Question 597542: a total of 1200 yards of fencing is to be used to enclose a rectangular part of lot that boders a river. No fence is needed along the river.
a)write the equation that gives the relationship between the length, the width and the 1200 yards of fencing available.
b)the formula for the area of a rectangle(as the one enclosed by the fencing) is given by A=lw, where l is the length and w is the width. Solve the equation found in part(a) for l, and then use the result to write the area in terms of w only.
c)make a table with at least 6 possible values of the width w and the associated area A.
d)from the pattern found in part (c), what is the largest possible area that can be enclosed by 1200 yards of fencing?
e)find the maximum area that can be enclosed.
I really need help with this question, i am struggling badly with math. Please help me. Thank you for your time and effort.
marisol
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A total of 1200 yards of fencing is to be used to enclose a rectangular part of lot that borders a river.
No fence is needed along the river.
;
a)write the equation that gives the relationship between the length, the width and the 1200 yards of fencing available.
:
This would be the perimeter minus the side along the river
L + 2W = 1200
L = 1200 - 2W
:
b)the formula for the area of a rectangle(as the one enclosed by the fencing) is given by A=lw, where l is the length and w is the width.
Solve the equation found in part(a) for l, and then use the result to write the area in terms of w only.
This would be A = L*W
From part (a), we know L = (1200-2W), replace L with (1200-2W) in the Area equation
A = (1200-2w)*W
which is
A = -2W^2 + 1200W
:
c)make a table with at least 6 possible values of the width w and the associated area A.
Let's make a table using every 100 ft, up to 600 ft
Substitute 100' in the above equation and find A, same with 200, 300, etc
Width|Area
------------
100|100000
200|160000
300|180000
400|160000
500|
600|
You should be able to complete this table, if I explained this sufficiently.
:
d)from the pattern found in part (c), what is the largest possible area that can be enclosed by 1200 yards of fencing?
You should be able note that the maximum area is 180000 when W = 300'
;
e)find the maximum area that can be enclosed.
This should be apparent by the table we just made, but there is a way to find the maximum of a quadratic equation like this one, using a formula x=-b/(2a)
In this equation x=W, a=-2, b= 1200, therefore
W = 
W = 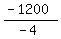
W = +300, is width that will give max area
Find the Max by substituting 300 for W in the equation
A = -2(300^2) + 1200(300)
A = -2(90000) + 360000
A = -180000 + 360000
A = 180000 sq/ft is the max area, agrees with what we found in our table
:
:
Perhaps this will be the beginning of the end of your struggles, Marisol, (which is a great a name). If you have any questions use the comment section to me.
|
|
|