SOLUTION: A mother has two children whose ages differ by 5 years. The sum of the squares of their ages is 97. The square of the mother’s age can be found by writing the square of the childre

Let the younger child's age = x
Then the older child's age = x+5

           x² + (x+5)² = 97

       x² + (x+5)(x+5) = 97

x² + x² + 5x + 5x + 25 = 97
    
        2x² + 10x + 25 = 97

        2x² + 10x - 72 = 0

Divide through by 2

          x² + 5x - 36 = 0

Factor

        (x + 9)(x - 4) = 0

Use the zero-factor principle:

   x + 9 = 0;       x - 4 = 0  
       x = -9;          x = 4

Ignore the negative answer. 

The younger child is 4.
The older child is 5 years older or 9.

The square of the younger child's age = 4² = 16

The square of the older child's age = 9² = 81

Four-digit number = 1681 so,

The square of the mother's age is 1681.

The mother's age = 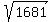  = 41

Edwin