SOLUTION: Please show work because the answer I am coming up with is not correct.Please help me. The terminal is 30ft down the 10-ft driveway and on the other side. A contractor charges

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Please show work because the answer I am coming up with is not correct.Please help me. The terminal is 30ft down the 10-ft driveway and on the other side. A contractor charges       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 588892: Please show work because the answer I am coming up with is not correct.Please help me.
The terminal is 30ft down the 10-ft driveway and on the other side. A contractor charges $3/ft alongside the driveway and $4/ft for underneath the driveway.
a. What will it cost if the contractor runs the pipe entirely under the driveway along the diagonal of the 30-ft by 10ft rectangle.
b. What will it cost if the contractor runs the pipe 30ft alongside the driveway and the 10ft straight across?
c. The contractor claims that he can doo the job for $120 by going alongside the driveway for some distance and then going under the drive diagonally to the terminal.Find x, the distance along side the driveway.
d. Write the cost as a function fo x and sketch the graph of the function.
e. Use the minimum feature of a graphing calcutor to find the appropriate value for x that will minimize the cost.
f. What is the minimum cost (to the nearest cent)of which the job can be done.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
a. The length of the diagonal of the 30-ft by 10ft rectangle, in feet, is
sqrt%2830%5E2%2B10%5E2%29=sqrt%28900%2B100%29=sqrt%281000%29=10sqrt%2810%29
The cost if the contractor runs the pipe entirely under the driveway would be $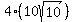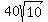4%2A%2810sqrt%2810%29%29=$40sqrt%2810%29 (approx $126.49)
b. If the contractor runs the pipe 30ft alongside the driveway and the 10ft straight across, the cost would be
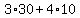$3%2A30%2B4%2A10=$90%2B40=$130
d. Going alongside the driveway for some distance, x, and then going under the drive diagonally to the terminal would include a distance, in feet, under the driveway of
sqrt%28%2830-3%29%5E2%2B10%5E2%29=sqrt%28900-60x%2Bx%5E2%2B100%29=sqrt%28x%5E2-60x%2B1000%29.
The cost, in $, would be C%28x%29=3x%2B4sqrt%28x%5E2-60x%2B1000%29.
graph%28300%2C300%2C-5%2C30%2C-10%2C140%2C3x%2B4sqrt%28x%5E2-60x%2B1000%29%29
c. The contractor claims that he can doo the job for $120 by going longside the driveway for some distance, x, and then going under the drive diagonally.
That means
120=3x%2B4sqrt%28x%5E2-60x%2B1000%29 --> 120-3x=4sqrt%28x%5E2-60x%2B1000%29 --> %28120-3x%29%5E2=16%28x%5E2-60x%2B1000%29 --> 1440-720x%2B9x%5E2=16x%5E2-960x%2B16000 --> 7x%5E2-240x%2B1600=0
Applying the quadratic formula,
(approximately 9.06 and 25.22 ft)
e. Use the minimum feature of a graphing calcutor to find the appropriate value for x that will minimize the cost. I do not have a graphing calculator handy but calculus says it's about 18.66 ft.
f. What is the minimum cost (to the nearest cent)of which the job can be done.
$116.46 according to my calculations