Question 58873: Steve traveled 600 miles at a certain speed. Had he gone 20mph faster, the trip would have taken 1 hour less. Find the speed of his vehicle.
This is what I have...Using distance formula d=rt (distance=rate x time) here.
Let x=Steve's speed (or rate). Using distance formula d=rt and solving for time, t=d/r. So since Steve's speed is x and distance is 600 miles, then Steve's time is 600/x. Steve's trip would have been 1 hour less if his speed was 20mph faster, or x+20. Distance is still 600 miles, so Steve's faster time would have been 600/(x+20). So the equation is to take the expression for Steve's actual time, subtract 1 from that, and set equal to his faster time. Solve for x.
Im stuck now
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Steve traveled 600 miles at a certain speed. Had he gone 20mph faster, the trip would have taken 1 hour less. Find the speed of his vehicle.
:
you have the right idea:
Original time - 1 hr = time going faster
The equation as you stated it:
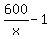 = = 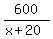
:
To solve for x you must get rid of those denominators, you do this by mult the
equation by x(x+20), a common denominator, you then have:
:
600(x+20) - 1(x(x+20) = 600x
:
600x + 12000 - x^2 - 20x = 600x
:
-x^2 + 600x - 600x - 20x + 12000 = 0
:
-x^2 - 20x + 12000 = 0
:
x^2 + 20x - 12000 = 0; Mult eq by -1, easier to factor when x^2 is positive
:
Factors to:
(x + 120)(x - 100) = 0
:
x = +100, the positive solution is what we want here:
:
:
We can check that using time:
(600/100) - 1 = (600/120)
6 - 1 = 5
|
|
|