SOLUTION: when its digits are reversed, a particular positive two-digit integer is increased by 20%. What is the original number?

(reversed no.) = (original no.) + (20% of original no.)  

         10u+t = 10t+u + .20(10t+u)

       10u + t = 10t + u + 2t + .2u

Multiply through by 10

    100u + 10t = 100t + 10u + 20t + 2u
    100u + 10t = 120t + 12u 
           88u = 110t
          
             u = 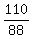t
             u = t
              = 

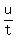The only possibility is for the units digit, u, to be 5,
and the tens digit, t, to be 4.  Therefore the number is 45.

The the digits of 45 are reversed, you get 54, an increase
of 9.  And 9 is 20% of 45.

Edwin