Question 482393: Simplifying by collecting like terms: I have a math problem that reads: Subtract the sum of -3m and -6p from their difference. My teacher says the answer is -12p. I am having trouble understanding the wording and setting up the problem. Can you help me solve this?
Thank you!
Found 4 solutions by Earlsdon, Edwin McCravy, kingme18, MathTherapy:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Your teacher is wrong. It's 12p, not -12p.
------------------------------------------
Subtract the sum of -3m and -6p from their difference.
-----------------------------------------
You are to subtract their sum from their difference.
Let's find their sum:
To find the sum write them down in parentheses and put a +
sign between them, like this:
(-3m) + (-6p)
then simplify that:
-3m-6p
------------------------------------------
Next let's find their difference:
To find the difference write them down in parentheses and put a -
sign between them, like this:
(-3m) - (-6p)
then simplify that:
-3m+6p
--------------------------------------------
Finally we need to subtract the sum FROM the difference.
When you subtract one amount from another, you always start with
the amount you're subtracting FROM and then you subtract from it.
Since we are subtracting FROM the difference, we write the difference
-3m+6p down first in parentheses, then we write the sum next in
parentheses, and put a - between them like this:
(-3m+6p) - (-3m-6p)
Then we simplify:
-3m + 6p + 3m + 6p
12p
So it comes out 12p, not -12p.
Edwin
Answer by kingme18(98)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is definitely interesting wording!
Your problem: subtract the sum of -3m and -6p from their difference.
Since the first thing it says is subtract, we know we're going to have to subtract two things. One of these is "the sum of -3m and -6p". "Sum" means add, so that means 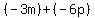 , or if you prefer, , or if you prefer, 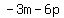 . The other thing is their difference, which means subtraction. The difference of -3m and -6p is . The other thing is their difference, which means subtraction. The difference of -3m and -6p is 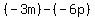 ; recall that a double negative (minus a negative) is the same as a positive, so ; recall that a double negative (minus a negative) is the same as a positive, so 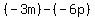 is the same as is the same as 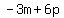 . .
Now we've dealt with "the sum of -3m and -6p" and "their difference". Last, we need to subtract the first thing FROM the second thing; that means we need to rearrange those groups. As an example: if I say "subtract 3 from 5", you'll do 5-3=2, not 3-5=-2. So we'll rearrange... Instead of the order the question puts it in (sum - difference), we'll flip. Thus, we'll do difference from above (simplified: 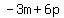 ) - sum from above (simplified: ) - sum from above (simplified: 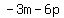 ): ): 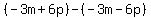 . I used parentheses there because we need to distribute the subtraction: . I used parentheses there because we need to distribute the subtraction: 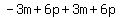 . The -3m and 3m cancel, and . The -3m and 3m cancel, and  . Your answer is 12p. . Your answer is 12p.
I talked to another math teacher, who agrees that this is 12p, not -12p. My guess is that your teacher didn't rearrange when subtracting (again, subtracting FROM something means to switch the order).
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! Simplifying by collecting like terms: I have a math problem that reads: Subtract the sum of -3m and -6p from their difference. My teacher says the answer is -12p. I am having trouble understanding the wording and setting up the problem. Can you help me solve this?
Thank you!
Subtract the sum of -3m and - 6p
the sum of - 3m and - 6p ------> - 3m + (- 6p) -------> - 3m - 6p
Their difference: - 3m - (- 6p) -------> - 3m + 6p
Since you're told to subtract the sum (- 3m - 6p) from the difference (- 3m + 6p), then we'll have: - 3m + 6p - (- 3m - 6p), which gives us: - 3m + 6p + 3m + 6p = - 3m + 3m + 6p + 6p = 
I agree with the other two tutors in that the teacher is incorrect, as the answer is in fact: 
|
|
|