Question 47898: A rectangular enclosure must have an area of at least 900yd^2. If 200yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie?
Answer by pizza(14)   (Show Source): (Show Source):
You can put this solution on YOUR website! Not so easy, this one.
I shall assume you know your algebra, and do not require much explanation.
Otherwise, you have to feedback and I will edit my solution.
First, let us set up the problem.
Let w be the width and l be the length.
Then we have
(1): wl > 900
(2): 2w + 2l = 200
From the second equation, we get l = 100 - w,
which put into the first equation gives w(100-w) > 900
which expands out to 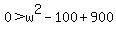
which factorises to be 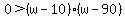
This implies, hopefully you can see why, that 10 < w < 90.
However, because w < l , we also have that w < 50,
from equation 2, or from l = 100-w.
Therefore, the answer is 10 < w < 50.
|
|
|