The other tutor's answer for the correct standard deviation is wrong.
Also he used the formula for the standard deviation of a sample, and
this student has informed me that this is to be considered as an
entire population, not as a sample from a population.
He gave:
4.5^2=20.25
20.25*22=445.5 sum of (each data point minus mean)^2
But that is the sum of each data point minus the mean of the 23)^2
not (the sum of each data point minus the mean of the 25)^2
He incorrectly assumed this was the latter.
It's a bit more complicated than what he did.
He used the definition of the standard deviation
of a sample
 but you must use the "shortcut" formula for the
standard deviation of a population
but you must use the "shortcut" formula for the
standard deviation of a population
 for the standard deviation instead.
Here is the entire correct problem:
-----------------------------------------------------------------
for the standard deviation instead.
Here is the entire correct problem:
-----------------------------------------------------------------
A certain set of data has a mean of 20 and a Standard deviation of 4.5. It is found that two pieces of data have been omitted, one of value 30 and the other of value 25. Find the mean and S.D of the full 25 pieces of data.
Let 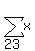 = the unknown sum of the 23 numbers
Let
= the unknown sum of the 23 numbers
Let  = the unknown sum of the 25 numbers
Then
(1)
= the unknown sum of the 25 numbers
Then
(1)  Let
Let  be the given mean of the 23 numbers
Let
be the given mean of the 23 numbers
Let 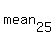 be the unknown mean of the 25 numbers.
Since
be the unknown mean of the 25 numbers.
Since  , then
, then
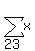
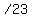

 Multiplying both side by 23 gives
Multiplying both side by 23 gives
 From equation (1) above
From equation (1) above
 Therefore
Therefore

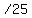

 That's the mean of the 25 numbers, which the other tutor
calculated correctly.
-----------------------------------
Now we use the short-cut formula for the standard deviation
of a population:
That's the mean of the 25 numbers, which the other tutor
calculated correctly.
-----------------------------------
Now we use the short-cut formula for the standard deviation
of a population:
 We will use the above formula with both sides squared,
for convenience:
We will use the above formula with both sides squared,
for convenience:
 Let
Let  be the given standard deviation of the 23 numbers
Let
be the given standard deviation of the 23 numbers
Let  be the unknown standard deviation of the 25 numbers
Let
be the unknown standard deviation of the 25 numbers
Let 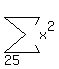 be the unknown sum of the squares of the 25 numbers.
Therefore,
(2)
be the unknown sum of the squares of the 25 numbers.
Therefore,
(2)  Using the formula for the 23 numbers:
Using the formula for the 23 numbers:
 Substituting given values,
Substituting given values,


 Multiply both sides by 23
Multiply both sides by 23
 From equation (2) above,
From equation (2) above,
 Using the formula for the 25 numbers,
Using the formula for the 25 numbers,
 Substituting known values
Substituting known values




 Edwin
Edwin