SOLUTION: If a stone is tossed from the top of a 230 meter building, the height of the stone as a function of time is given by h(t) = -9.8t2 – 10t + 230, where t is in seconds, and height i

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: If a stone is tossed from the top of a 230 meter building, the height of the stone as a function of time is given by h(t) = -9.8t2 – 10t + 230, where t is in seconds, and height i      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 366047: If a stone is tossed from the top of a 230 meter building, the height of the stone as a function of time is given by h(t) = -9.8t2 – 10t + 230, where t is in seconds, and height is in meters. After how many seconds will the stone hit the ground? Round to the nearest hundredth’s place; include units in your answer.
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
It hits the ground when h(t) = 0.
Solve the equation for t.
----------------
h(t) = -9.8t2 – 10t + 230 = 0
------------------
If this happens on Earth, it should be h(t) = -4.9t^2 – 10t + 230, not 9.8t^2
------------------
Using 9.8:
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case -9.8x%5E2%2B-10x%2B230+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-10%29%5E2-4%2A-9.8%2A230=9116.

Discriminant d=9116 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--10%2B-sqrt%28+9116+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-10%29%2Bsqrt%28+9116+%29%29%2F2%5C-9.8+=+-5.38151765807347
x%5B2%5D+=+%28-%28-10%29-sqrt%28+9116+%29%29%2F2%5C-9.8+=+4.36110949480817

Quadratic expression 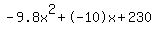-9.8x%5E2%2B-10x%2B230 can be factored:
-9.8x%5E2%2B-10x%2B230+=+%28x--5.38151765807347%29%2A%28x-4.36110949480817%29
Again, the answer is: -5.38151765807347, 4.36110949480817. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-9.8%2Ax%5E2%2B-10%2Ax%2B230+%29

------------
Using 4.9:
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case -4.9x%5E2%2B-10x%2B230+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-10%29%5E2-4%2A-4.9%2A230=4608.

Discriminant d=4608 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--10%2B-sqrt%28+4608+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-10%29%2Bsqrt%28+4608+%29%29%2F2%5C-4.9+=+-7.94716846876618
x%5B2%5D+=+%28-%28-10%29-sqrt%28+4608+%29%29%2F2%5C-4.9+=+5.90635214223557

Quadratic expression 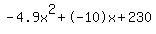-4.9x%5E2%2B-10x%2B230 can be factored:
-4.9x%5E2%2B-10x%2B230+=+%28x--7.94716846876618%29%2A%28x-5.90635214223557%29
Again, the answer is: -7.94716846876618, 5.90635214223557. Here's your graph:
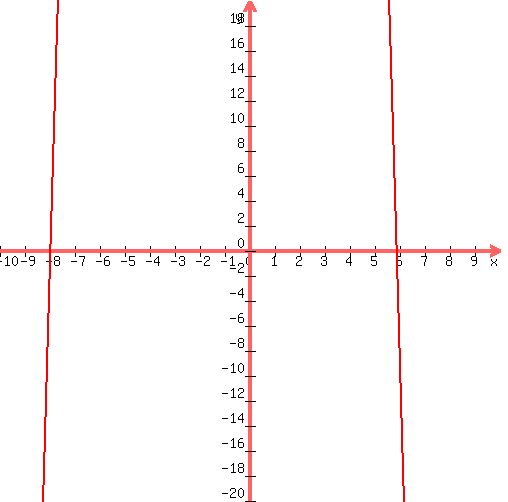graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-4.9%2Ax%5E2%2B-10%2Ax%2B230+%29

--------------
Ignore the negative values.
t = x in seconds