Question 180469: Lisa and Ted agree to meet at the construction site located 100 miles from Norwood on the 300 mile highway connecting Norwood to Huntsville. Lisa leaves Huntsville at noon while Ted departs from Norwood one hour later. If they arrive at the construction site simotaniously and Lisa's driving speed averaged 10mph faster than Ted's, than how fast did she drive?
Answer by Mathtut(3670)   (Show Source): (Show Source):
You can put this solution on YOUR website! Lisa and Ted agree to meet at the construction site located 100 miles from Norwood on the 300 mile highway connecting Norwood to Huntsville. Lisa leaves Huntsville at noon while Ted departs from Norwood one hour later. If they arrive at the construction site simotaniously and Lisa's driving speed averaged 10mph faster than Ted's, than how fast did she drive?
:
lets call the Ted's rate r ,his time is t, and his distance is 100
..............Lisa's rate is r+10, her time is t+1, and her distance is 200
:
Ted: 100=rt............eq 1
Lisa:200=(r+10)(t+1)...eq 2
:
take eq 1 and rewrite to t=100/r and plug that value into eq 2
:
200=(r+10)((100/r)+1)
:
200=(r+10)((100+r)/r)...used r as the common denominator of term and combined
:
the numerators
:
200r==(r+10)((100+r)......multiplied both sides by r to eliminate the fraction
:

:
 }set up as a quadratic equation }set up as a quadratic equation
:
r=77 and 13 rounded
:
Lisa is r+10 so she drove either 23 mph or 87 mph
:
13 and 23 doesnt seem reasonable on a highway so you could throw that out
on that basis.
:
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=4100 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 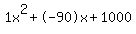 can be factored: can be factored:

Again, the answer is: 77.0156211871642, 12.9843788128358.
Here's your graph:
 |
|
|
|