Question 169784: If ine side of a right triangle is 12 and its hypotenuse is 13, what is the length of the other side?
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
If one side of a right triangle is 12 and its hypotenuse is 13, what is the length of the other side?
.
The formula to find the Hypotenuse or sides is  , where "a" and "b" are the sides, and "c" is the hypotenuse , where "a" and "b" are the sides, and "c" is the hypotenuse
.
We can replace "c" with the length of the hypotenuse (13), and we can replace "a" or "b" with "12" ( we will replace "a" )
.
a = 12
.
b = unknown
.
c = 13
.
 = =  = = 
.
We will now move "144" to the right side
.
 = =  = =  , now we just take the square root of both sides , now we just take the square root of both sides
.
 = =  = =  or or 
.
Since lengths cannot be nagative, the length of the other side is "5"
.
You can check by replacing "b" with "5" in the equation
.
 = =  = =  = =  , (True) , (True)
.
The length of the other side is "5"
.
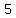 is your answer is your answer
.
Hope I helped, Levi
|
|
|