Question 139185: A projectile is fired from a cliff 200 feet above the water at an inclination of 45 degrees to the horizontal, with a muzzle velocity of 50 feet per second. The height h of the projectile above the water is given by
h(x)=-32x^2/(50)^2+x+200
where x is the horizontal distance of the projectile from the base of the cliff.
a.)Explain how you know whether the height function obtains a maximum or minimum.
b.)How far from the base of the cliff is the height of the projectile a maximum?
c.)Explain what you are finding if you solve the equation below.
-32x^2/(50)^2+x+200=0
d.)Solve the equation in part c.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) the graph of the function is a parabola. since the lead coefficient is negative, the parabola opens downward, meaning the vertex is a maximum of the function. If you need the calculus solution, the second derivitive is 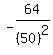 , so it is everywhere negative in the domain of the function, hence the extreme point is a maximum. , so it is everywhere negative in the domain of the function, hence the extreme point is a maximum.
b) The x-coordinate of the vertex of any parabola in the form  is given by is given by 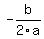 . So evaluate . So evaluate 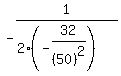 to find the value of x, i.e. the horizontal distance, at the vertex, or maximum. to find the value of x, i.e. the horizontal distance, at the vertex, or maximum.
c) If the the function represents the height above the water of the projectile for any given horizontal distance, and if that height is zero, then the projectile is impacting the water. So setting the function equal to zero and solving for x gives you the horizontal distance from the base of the cliff to the point of impact with the water. Hopefully, the enemy ship is in the same place -- but that is just an old sailor talking.
|
|
|