Question 131525: Hello the chapter im working on is called exponential and logarithmic functions. The section is on exploring exponential models. Could you help me with this exponential growth word problem on bacteria?
Here it is:
A scientist notes the bacteria count in a petrie dish is 50. Two hours later, he notes the count has increased to 80. If this rate of growth continues, how much more time will it take for the bacteria count to reach 100?
THanks for the help and time
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hello the chapter im working on is called exponential and logarithmic functions. The section is on exploring exponential models. Could you help me with this exponential growth word problem on bacteria?
Here it is:
A scientist notes the bacteria count in a petrie dish is 50. Two hours later, he notes the count has increased to 80. If this rate of growth continues, how much more time will it take for the bacteria count to reach 100?
THanks for the help and time
The formula spells the word "Pert"
A = Pert
At time t = 0, the amount of bacteria in the dish, A, is 50.
Substituting:
50 = Pert
50 = Per(0)
50 = Pe0
50 = P(1)
50 = P
So the formula A = Pert
is now
A = 50ert
>>...Two hours later, he notes the count has increased to 80...<<
Therefore, at time t = 2, the amount of bacteria in the dish, A, is 80.
Substituting:
80 = 50ert
80 = 50er(2)
80 = 50e2r
Divide both sides by 50
 = e2r
1.6 = e2r
Use the definition formula for
a natural logarithm:
M = eN is equivalent to ln(M) = N
So
1.6 = e2r
becomes
ln(1.6) = 2r
Use a calculator to find ln(1.6) = 0.4700036292,
rounding to 0.470
0.470 = 2r
Divide both sides by 2
0.235 = r
Now the formula
A = 50ert
becomes
A = 50e0.235t
Now the question is:
>>...how much more time will it take for
the bacteria count to reach 100?...<<
We substitute 100 for A and solve for t
100 = 50e0.235t
Divide both sides by 50 = e2r
1.6 = e2r
Use the definition formula for
a natural logarithm:
M = eN is equivalent to ln(M) = N
So
1.6 = e2r
becomes
ln(1.6) = 2r
Use a calculator to find ln(1.6) = 0.4700036292,
rounding to 0.470
0.470 = 2r
Divide both sides by 2
0.235 = r
Now the formula
A = 50ert
becomes
A = 50e0.235t
Now the question is:
>>...how much more time will it take for
the bacteria count to reach 100?...<<
We substitute 100 for A and solve for t
100 = 50e0.235t
Divide both sides by 50
 = e0.235t
2 = e0.235t
Use the definition formula again for
a natural logarithm:
M = eN is equivalent to ln(M) = N
So
ln(2) = 0.235t
Get ln(2) from calculator as 0.6931471806, rounding
to 0.693
0.693 = 0.235t
Divide both sides by 0.235 = e0.235t
2 = e0.235t
Use the definition formula again for
a natural logarithm:
M = eN is equivalent to ln(M) = N
So
ln(2) = 0.235t
Get ln(2) from calculator as 0.6931471806, rounding
to 0.693
0.693 = 0.235t
Divide both sides by 0.235
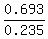 = t
2.95 = t
Multiplying 60 minutes times the decimal
part, .95, gives 57 minutes, so
It takes about 2 hours and 57 minutes.
However since the question asks "how much MORE time",
the answer is 57 minutes.
Edwin = t
2.95 = t
Multiplying 60 minutes times the decimal
part, .95, gives 57 minutes, so
It takes about 2 hours and 57 minutes.
However since the question asks "how much MORE time",
the answer is 57 minutes.
Edwin
|
|
|