Question 127546: I have been working on this problem for an hour now and I just don't get it. I would really appreciate some help.
One lemon costs one fils.
One orange costs twenty fils.
One apple costs fifty fils.
You need to buy a total for 100 fruits and 1 Kuwait Dinar (1000 fils in total) How many of each fruit will you buy?
Thanks a lot!
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! Number of lemons: l
Number of oranges: o
Number of apples: a
You need to buy 100 pieces of fruit, so 
The value of the lemons you buy, since they cost 1 fil each, is just l.
The value of the oranges is 20o
The value of the apples is 50a
The total value must be 1000 fils.
So, 
But now you are stuck because you don't have any other information. You have three unknown quantities, but only two equations. However, you actually do have more information, it is just hidden a bit.
Since apples cost 50 fils, the most you could buy would be  , but then you would only have 20 pieces of fruit and no money to buy anything else. So we know the answer must have a value for apples that is a good deal less than 20.
Let's see what happens if we buy no apples at all:
From our original set of equations:
 , and
Case: 
 , and
Multiply the first equation by -1
Add it to the second equation:
Since you can't buy a fractional part of an orange, this answer can be excluded.
Let's divide and conquer:
Case 
 , and
Multiply by -1 again:
 and we get another fractional result. Hmmm. What are the possibilities?
If you take all the possibilities for the number of apples purchased, 19 times the number of oranges must be equal to  . So for all possible values of a, and we know that a > 0 and a < 20, what are the values of  ?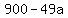
Here's a list from a = 1 to a = 18.
851
802
753
704
655
606
557
508
459
410
361
312
263
214
165
116
67
18
The question becomes which of these numbers is evenly divisible by 19?
I'll save you a little calculator work: it is 361, which equates to a = 11.
Case 
 , and
Multiply by -1 again:
So we have 11 apples, 19 oranges, and  lemons.
Check: 11 apples @ 50 = 550, 19 oranges @ 20 = 380, and 70 lemons @ 1 = 70
 and 
Answer checks.
|
|
|
