Question 1210368: إذا كانت A,Bمجموعتان غير خاليتان من Rومحدودتان أثبت أن
inf (A+B) = inf A + inf B
Answer by ikleyn(53422)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Google translation to English:
If A, B are two non-empty sets of R and bounded, prove that
inf (A+B) = inf A + inf B
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The proof consists of two parts.
First part of the proof
Let a = inf(A), b = inf(B).
Since the subsets A and B are bounded in R, the values 'a' and 'b' do exist and are defined properly.
The fact that a = inf(A) means that there is an infinite sequence 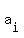 of elements of elements 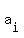 in A
which converges to 'a'.
The fact that b = inf(B) means that there is an infinite sequence in A
which converges to 'a'.
The fact that b = inf(B) means that there is an infinite sequence 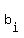 of elements of elements 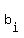 in B
which converges to 'b'.
Then the sequence in B
which converges to 'b'.
Then the sequence 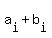 converges to value a+b.
This simple elementary statement is easy to prove.
It implies that
inf(A+B) <= a+b. (1)
Second part of the proof
Again, let a = inf(A), b = inf(B).
Since the subsets A and B are bounded in R, the values 'a' and 'b' do exist and are defined properly.
Since the subsets A and B are bounded in R, the set of all real numbers of the form {x+y),
where x is from A and y is from B, is bounded, too.
Hence, the set of all sums (x+y) has the infinum. Let z = inf(A+B).
The fact that z = inf(A+B) means that there is an infinite sequence converges to value a+b.
This simple elementary statement is easy to prove.
It implies that
inf(A+B) <= a+b. (1)
Second part of the proof
Again, let a = inf(A), b = inf(B).
Since the subsets A and B are bounded in R, the values 'a' and 'b' do exist and are defined properly.
Since the subsets A and B are bounded in R, the set of all real numbers of the form {x+y),
where x is from A and y is from B, is bounded, too.
Hence, the set of all sums (x+y) has the infinum. Let z = inf(A+B).
The fact that z = inf(A+B) means that there is an infinite sequence 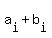 with elements
with elements 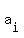 in A and in A and 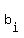 in B, which converges to z.
Notice that all in B, which converges to z.
Notice that all 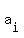 are not less than 'a', and all are not less than 'a', and all 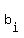 are not less than 'b',
due to the definitions of 'a' and 'b'.
It means that
z = inf(A+B) = ( lim are not less than 'b',
due to the definitions of 'a' and 'b'.
It means that
z = inf(A+B) = ( lim  as i --> as i -->  ) >= a + b = inf(A) + inf(B). (2).
Inequalities (1) and (2), taken together, prove that
inf(A+B) = inf(A) + inf(B).
QED. ) >= a + b = inf(A) + inf(B). (2).
Inequalities (1) and (2), taken together, prove that
inf(A+B) = inf(A) + inf(B).
QED.
Solved, proved and completed.
|
|
|