Question 1209275: On a day when visibility was limited to 2500 m, a ship of the Blue Line was traveling west, on a parallel course to a ship of the White Line traveling east, with the courses 700 m apart. The Blue Line ship's velocity was 10 km/h. If the ships were in sight of each other for 20 minutes, what was the velocity, in km/h, of the White Line ship?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52898)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
On a day when visibility was limited to 2500 m, a ship of the Blue Line was traveling west,
on a parallel course to a ship of the White Line traveling east, with the courses 700 m apart.
The Blue Line ship's velocity was 10 km/h. If the ships were in sight of each other for 20 minutes,
what was the velocity, in km/h, of the White Line ship?
~~~~~~~~~~~~~~~~~~
According to the problem, we have two parallel number lines in the ocean,
that represent the courses.
Let's think that the origins in both lines are chosen that way that they are
located on the shortest distance of 700 meters between them.
Let  be the coordinate of the Blue line ship, and
Let be the coordinate of the Blue line ship, and
Let  be the coordinate of the White line ship.
Then, from right angled triangles, the condition of visibility is this inequality be the coordinate of the White line ship.
Then, from right angled triangles, the condition of visibility is this inequality
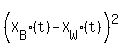 + +  <= 2500^2 meters,
or <= 2500^2 meters,
or
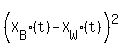 <= 2500^2 - 700^2, <= 2500^2 - 700^2,
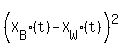 <= 5760000, <= 5760000,
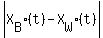 <= <=  , ,
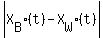 <= 2400,
-2400 <= <= 2400,
-2400 <= 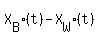 <= 2400. (1)
In this inequality, <= 2400. (1)
In this inequality,  = -10000*t meters, = -10000*t meters,  = w*t, where w is the constant speed
of the West line ship, w = 10 km/h = 10000 m/h. We take the speed -10000 m/h negative since this ship travels west.
So, inequality (1) takes the form
-2400 <= -10000t - wt <= 2400. (2) (in meters)
First time they see each other at
-10000*t1 - w*t1 = 2400. (3)
Last time they see each other at
-10000*t2 - w*t2 = -2400. (4)
Subtract equation (3) from equation (2)
-10000*(t2-t1) - w(t2-t1) = -4800.
Substitute here t2 - t1 = 20 minutes, or (1/3) of an hour; w = 10 km/h = 10000 m/h. You will get = w*t, where w is the constant speed
of the West line ship, w = 10 km/h = 10000 m/h. We take the speed -10000 m/h negative since this ship travels west.
So, inequality (1) takes the form
-2400 <= -10000t - wt <= 2400. (2) (in meters)
First time they see each other at
-10000*t1 - w*t1 = 2400. (3)
Last time they see each other at
-10000*t2 - w*t2 = -2400. (4)
Subtract equation (3) from equation (2)
-10000*(t2-t1) - w(t2-t1) = -4800.
Substitute here t2 - t1 = 20 minutes, or (1/3) of an hour; w = 10 km/h = 10000 m/h. You will get
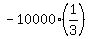 - -  = -4800,
10000 + w = 4800*3,
4800*3 - 3 = w,
w = 4400 m/h or 4.4 kilometers per hour.
ANSWER. The speed of the White Line ship is 4.4 kilometers per hour. = -4800,
10000 + w = 4800*3,
4800*3 - 3 = w,
w = 4400 m/h or 4.4 kilometers per hour.
ANSWER. The speed of the White Line ship is 4.4 kilometers per hour.
Solved.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 4.4 km/hr to the east
--------------------------------------------------------------------------
Explanation
To convert from meters to kilometers, we divide by 1000.
2500 meters = 2500/1000 = 2.5 km is one example
To convert from minutes to hours, divide by 60
20 min = 20/60 = 1/3 of an hour
point B = blue ship
point W = white ship
At the start of this process let's place point B at the origin (0,0)
This ship travels west along the horizontal line y = 0, aka the x axis.
Meanwhile the white ship travels east along the horizontal line y = 0.7; which allows the two parallel paths to be spaced 0.7 km apart.
Draw a circle centered at B with radius 2.5
This circle has the equation x^2+y^2 = 6.25
The 6.25 is the result of computing (2.5)^2
After plugging in y = 0.7, you should go from x^2+y^2 = 6.25 to x = -2.4 and x = 2.4 as the two solutions.
I'll let the student handle the scratch work.
Place point W at (-2.4, 0.7) which is where the blue ship starts to see the white ship.
Note that W is on the line y = 0.7 and on the circle. Also, W is to the left of B at the start.
If W started to the right of B, then the window of visibility would be far less than 20 minutes.
This is why we disregard the x = 2.4 case.
--------------------------------------------------------------------------
To recap so far
B starts at (0,0)
W starts at (-2.4, 0.7)
The decimal coordinates for point W are exact.
Let variable t represent the number of hours that elapse after the two ships are in view of one another.
After t hours, B moves from (0,0) to (-10t, 0) since it's traveling 10 km/hr to the west.
W moves from (-2.4, 0.7) to (-2.4+vt, 0.7) where v is the velocity of the white ship in km/hr.
If t = 1/3 of an hour goes by, then B will end up at
B = (-10t, 0) = (-10*(1/3), 0) = (-10/3, 0) = (-3.3333, 0) approximately
The 3's in that decimal value go on forever.
Once B arrives at its ending location, lets form another circle equation centered at (-10/3, 0) with the same radius 2.5 km.
That equation would be (x+10/3)^2 + y^2 = 6.25
Like earlier, plug in y = 0.7 and solve for x (the scratch work will be left for the student).
You should go from (x+10/3)^2 + y^2 = 6.25 to these solutions
x = -86/15 = -5.7333333...
x = -14/15 = -0.9333333...
The 3's go on forever in those decimal values.
Select the larger x value since W will be to the right of B when t = 1/3 of an hour has elapsed.
It wouldn't make much sense to have W be to the left of B at this moment in time.
B goes from (0,0) to (-10/3, 0)
W goes from (-2.4, 0.7) to (-14/15, 0.7)
We'll set the x coordinate -14/15 equal to the expression -2.4+vt so we can determine v.
-2.4+vt = -14/15
-2.4+v*(1/3) = -14/15
-24/10+(1/3)v = -14/15
-12/5+(1/3)v = -14/15
15*( -12/5+(1/3)v ) = 15*( -14/15 )
-36 + 5v = -14
5v = -14+36
5v = 22
v = 22/5
v = 4.4
The White Line ship's velocity is 4.4 km/hr to the east
Here is an interactive GeoGebra applet which helps confirm the answer.
https://www.geogebra.org/calculator/umbyvbaq
Move the slider for parameter t so you can see how the ships are moving.
|
|
|