Question 1208983: A triangle with sides of 21 cm, 72 cm and 75 cm is cut into parts that form a quadrilateral. Find, in cm2, the area of the largest quadrilateral that can be formed.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A triangle with sides of 21 cm, 72 cm and 75 cm is cut into parts that form a quadrilateral.
Find, in cm2, the area of the largest quadrilateral that can be formed.
~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, it is assumed that the quadrilateral is formed of disjoint parts
of the triangle with no holes (empty spaces) and without overlaying.
Then the area of the quadrilateral is equal to the area of the original triangle.
The area of the original triangle can be found using the Heron's formula
S = 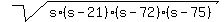 , where s is the semi-perimeter s = , where s is the semi-perimeter s =  = 84 cm.
So, for the area we have
S = = 84 cm.
So, for the area we have
S = 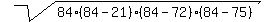 = = 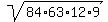 = 756 cm^2. ANSWER = 756 cm^2. ANSWER
Solved.
-----------------
By the way, it is easy to check that the triangle with the sides
21 cm, 72 cm and 75 cm is a right-angled triangle.
So, it gives another, more simple way to calculate its area 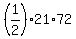 = 756 cm^2. = 756 cm^2.
|
|
|