SOLUTION: The pattern forming the irrational number 0.3450543003450005430000... continues indefinitely. What is the 81403rd digit in this pattern?

0.3450543003450005430000

I assume you meant digits AFTER the decimal, not including the introductory 0.

The 4's occur in positions 2, 6, 11, 17, ...

Its sequence of first differences 4, 5, 6,... is linear, so the
sequence of positions of 4s is quadratic.

Also if 4 has occurred an even-number of times, the digit that follows it is a
3, and if 4 has occurred an odd-number of times, the digit that follows it is a
5.

Let the general term of 2, 6, 11, 17, ... be 





Solve that and get A=0.5, B=2.5, C=-1

So the general term for the positions of 4's is 

So let's find the position of the 4 nearest the 81403rd term by setting





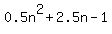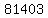
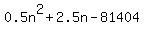Solving that with a quadratic program on my TI-84 graphing calculator:

n=401.0024783 and n=-406.0024783

So it is almost equivalent to a quadratic factorable as (n-401)(n+406) which
would have been this quadratic in n:



The first two terms of that are twice the first two terms of the general
equation for the positions of the 4's. So we divide through by 2



Adding 81403 to both sides



Adding -1 makes the left side the general term for digit positions of 
the 4's. So let's add -1 to the right side also:



That has solutions 401 and -406, so the 81402nd digit is a 4 and since 
it is the 401st occurrence of a 4, and 401 is odd, the next digit, or the
81403rd digit, is a 5.

BTW, if you did include the introductory 0 left of the decimal point, then the
answer would have been 4, and the solution would have been a little easier.

Edwin

In case you got my previous solution which had an error, 
before I corrected it, I have now corrected it above.

Edwin

0.3450543003450005430000

Here is the problem assuming the introductory 0 on the left of the decimal is the 1st digit

The 4's occur in positions 3, 7, 12, 18, ...

Its sequence of first differences 4, 5, 6,... is linear, so the
sequence of positions of 4s is quadratic.

Let the general term of 3, 7, 12, 18, ... be 





Solve that and get A=0.5, B=2.5, C=0

So the general term for the positions of 4's is 

So let's find the position of the 4 nearest (or 'at') the 81403rd term by 
setting





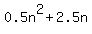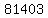
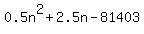Solving that with a quadratic program on my TI-84 graphing calculator:

n=401 and n=-406 

That has solution 401 (Ignore the negative), so the 81403rd digit is a 4.

Answer = 4

--------------------------------------------------------------

It's easier when we consider the 0 to the left of the decimal as the
first digit.

In the olden days, people didn't, as a rule, put a 0 before the decimal
in decimal fractions between -1 and 1, as they do today.  We would just write,
say, .5, not 0.5, and -.75, not -0.75 and:
  
.3450543003450005430000... not 0.3450543003450005430000...
 
I'm an old fogy, so that's why I didn't consider the initial 0 before
the decimal as the first digit in my other answer. LOL

Edwin