SOLUTION: An arithmetic series of 30 375 terms has a sum that is a perfect fifth power. What is the smallest positive sum of this series?

I think this is a trick question and one such arithmetic series 
could be:

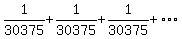 to 30375 terms 

with common difference d=0. It has a sum = 1 which is the 
smallest positive perfect 5th power.

There are other arithmetic series with 30375 terms and 
sum 1 with tiny first terms and tiny common differences 
greater than 0, but I see no reason the common difference 
can't be 0.
 
Edwin

The sum of this AP should be an integer positive number, which is a perfect fifth power.

The smallest integer positive number, which is a perfect fifth power is 1:  1 = .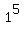


        I want to create an AP with 30375 terms, whose sum will be 1.


I will take c = 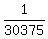  as the central term of this AP.

I will take an arbitrary real number d as the common difference of this AP.


    +--------------------------------------------------------------+
    |   I will take 15187 terms of this AP on the right from "c"   |
    |           and 15187 terms of this AP on the left from "c".   |
    +--------------------------------------------------------------+


             15187 is a remarkable number for this problem: 
                 it is about half of the number 30375.


When I will calculate the sum, the pairs of numbers c+kd and c-kd, equally remoted from the center, 
will give the sum of 2c; the parts "+kd" and "-kd" will cancel.


So, the sum of this my progression will be 

    central term c + 15187*(2c),  or  c*(1+2*15187) = 30375*c = 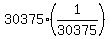 = 1.


    Thus, this AP will provide the answer: central term c =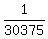   
        and the common difference d = an arbitrary real number.

          You should take 15187 terms on the right from "c" 
        and the same number, 15187 terms, on the left from "c".


The sum of all terms of this AP will be 1, which is the smallest positive integer perfect fifth power.


So, all the requirements are satisfied, and the solution is complete.

Post-solution note: