SOLUTION: What is the maximum number of bottles, each of diameter 9 cm, that can be packed into a box with a square base measuring 990 cm by 990 cm? The diagram below shows the closest packi

Let's consider this dense packing scheme, which is shown in the attached diagram.

First horizontal row of bottles will have  990 : 9 = 110 bottles.

The line of their centers is y = 4.5 cm.


The centers of the circles form a grid of equilateral triangles with the side length of 9 cm.


When the side of an equilateral triangle is a = 9 cm, its height/altitude is  

    h = 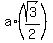 =  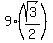= 7.79423 cm (rounded up).


So, the second row of circles is 7.79423 cm above the first horizontal line y = 4.5 cm.

Thus, the equation of the 2nd horizontal line of centers is  y = 4.5 + 7.79423,  or  y = 12.29423 cm.


The most upper horizontal line of circles is not closer than 4.5 cm to the upper bound y = 990 cm.


Therefore, if the total number of horizontal lines of centers is n, we can write this inequality

    4.5 + (n-1)*7.79423 + 4.5 <= 990  cm,

or

    (n-1)*7.79423 <= 990 - 4.5 - 4.5 = 990 - 9 = 981 cm.


S0, the number of lines is about (is not more than)

    n <= 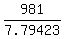 + 1 = 125.8623366 + 1.


Rounding to the closest lesser integer number, we see that

    n <= 126.


We see that there is the room for 126 lines of centers, but there is no room for 127 lines.


The number of bottles / (circles) in lines is altering  110, 109, 110, 109, . . . , 110, 109, 110, 109.


So, this sequence has 63 lines with 110 bottles and 63 lines with 109 bottles.


Hence, the total maximum possible number of bottles is  63*110 + 63*109 = 13797.


ANSWER.   The total maximum possible number of bottles in the box is  13,797.