Question 1208467: A movie hall sold tickets to one of its shows in two denominations, $11 and $7. A fourth of all those who bought a ticket also spent $4 each on refreshments at the movie hall. If the total collections from tickets and refreshments for the show was $124, how many $7 tickets were sold? Note: The number of $11 tickets sold is different from the number of $7 tickets sold.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
A movie hall sold tickets to one of its shows in two denominations, $11 and $7.
A fourth of all those who bought a ticket also spent $4 each on refreshments at the movie hall.
If the total collections from tickets and refreshments for the show was $124,
how many $7 tickets were sold?
Note: The number of $11 tickets sold is different from the number of $7 tickets sold.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the number of movie tickets sold at $11.
Let y be the number of movie tickets sold at $7.
We know that x+y, the total number of visitors, is a multiple of 4.
Also, we know that the total revenue was $124 and that x =/= y.
So, we write this equation for the total revenue
11x + 7y + 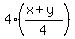 = 124, (1)
and we look for a solution to it in non-negative integer numbers such that and x=/= y and x+y is a multiple of 4.
We simplify equation (1)
12x + 8y = 124.
We re-write (2) in an equivalent form
x =  =  .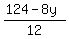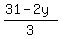
31 - 2y is divisible by 3 for y = 2, 5, 8, 11, 14, giving for x these values, respectively
9, 7, 5, 3, 1.
Thus we see that these pairs (x,y) = (9,2), (7,5), (5,8), (3,11), (1,14) are the potential solutions.
But then we check for the sum x+y to be a multiple of 4, and we see that the only a pair,
satisfying this condition, is (x,y) = (7,5).
ANSWER. 7 tickets at $11 and 5 tickets at $7 dollars.
CHECK. 7*11 + 5*7 + 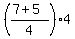 = 77 + 35 + 12 = 124 dollars as the total revenue, including refreshments. ! correct !
Solved.
--------------------
Notice that the condition x=/= y is excessive: it is not used in the solution.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
x = number of $11 tickets sold
y = number of $7 tickets sold
x+y = total number of tickets
0.25(x+y) = number of people who bought a refreshment
A = 11x = amount spent on the $11 tickets
B = 7y = amount spent on the $7 tickets
C = 4*0.25(x+y) = x+y = amount spent on refreshments
A+B+C = total amount spent
A+B+C = 124
11x+7y+x+y = 124
12x+8y = 124
4(3x+2y) = 124
3x+2y = 124/4
3x+2y = 31
Using trial-and-error, a graph, or the Extended Euclidean Algorithm, you will find these nonnegative integer solutions
(x, y) = (1, 14)
(x, y) = (3, 11)
(x, y) = (5, 8)
(x, y) = (7, 5)
(x, y) = (9, 2) Each time x goes up by 2, y decreases by 3.
Plug each of those coordinates into 0.25(x+y) to see which results in an integer.
(x,y) = (1, 14) ----> 0.25(x+y) = 0.25(1+14) = 0.25(15) = 3.75
(x,y) = (3, 11) ----> 0.25(x+y) = 0.25(3+11) = 0.25(14) = 3.5
(x,y) = (5, 8) -----> 0.25(x+y) = 0.25(5+8) = 0.25(13) = 3.25
(x,y) = (7, 5) -----> 0.25(x+y) = 0.25(7+5) = 0.25(12) = 3
(x,y) = (9, 2) -----> 0.25(x+y) = 0.25(9+2) = 0.25(11) = 2.75
Of those results only 3 is an integer. Everything else is a decimal value.
The result 3 corresponds to (x,y) = (7,5)
Another way to find this is to note that x+y = 7+5 = 12 is a multiple of 4. Every other sum is not a multiple of 4 (eg: x+y=1+14 = 15).
Question: how many $7 tickets were sold?
Answer: 5
|
|
|
