Question 1208226: Hi
A sheet of paper 42cm by 66cm has circles of 7cm radius cut out from it . What is the maximum number of circles that can be cut out from the paper.
Found 3 solutions by MathLover1, ikleyn, math_tutor2020:
Answer by MathLover1(20850)   (Show Source):
Answer by ikleyn(52808)  (Show Source):
You can put this solution on YOUR website! .
A sheet of paper 42cm by 66cm has circles of 7cm radius cut out from it.
What is the maximum number of circles that can be cut out from the paper.
~~~~~~~~~~~~~~~~~~~
To solve it in the way as @MathLover1 does it is the same
as to confess from the very beginning that you can not solve it
in a right way and even do not know how to direct your thoughts in a right way.
To solve it in a right way, think about most dense packing congruent circles in a plane.
Such packing is placing the centers of circles in vertices of equilateral triangle grid on the plane.
The side length of these equilateral triangles is, obviously, the diameter of these circles 2*7 = 14 cm.
So, we place first row of circles on the line parallel to the long side of the
rectangular piece of paper, placing their centers at the distance of 7 cm from the edge.
Four times the diameter is 4*14 = 56 cm, which is less than 66 cm; so we can place 4 circles this way.
But five times the diameter is 5*14 = 70, which is greater than 66 cm, so 5-th circle does not fit.
In this page of paper, construct a grid of equilateral triangles with the side of 14 cm
(which is the diameter of the circles).
So, one row of vertices is the centers of the first 4 circles, introduced above.
Next, second line of centers is the line remoted 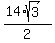 = 12.12436 cm approximately (rounded UP)
from the first line.
Let's estimate, how many circles can we place with the centers on the second line.
The center of the 1st circle will be 14 cm from the short edge, and the other centers will be placed
on the second line with the step of 14 cm.
With 4 circles in the second row, we will have the horizontal extension in the second row
14 + (14 + 14 + 14) + 7 = 63 cm, which is less than 66 cm.
From it, we see that it is possible to place 4 and only 4 such circles with the centers
on the second line.
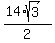Third line of the centers will be remoted = 12.12436 cm from the second line.
Since 7 + 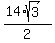+ + 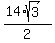7 = 38.24872 cm is less than 42 cm,
we see that the third row of circles fits vertically.
Thus, the conclusion from this reasoning is that 4 + 4 + 4 = 12 circles can be placed on / (or cut from)
the given list of paper, and this is the MAXIMUM possible number of circles.
Solved.
///////////////////////////
Again, if somebody will show to a teacher or at a competition the solution similar to that by @MathLover1,
it can only make the teacher / (the jury) smile, since this way of thinking is inadequate to the problem.
\\\\\\\\\\\\\\\\\\\\\\\\\\
I am very glad to see that tutor @math_tutor2020 developed in his post even better solution
than mine. I am also very glad to see that the general idea of considering
the most dense packing works so well in this problem.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
To get the densest packing possible, you'll need to arrange your circles into a hexagonal formation.
https://mathworld.wolfram.com/CirclePacking.html
Here is one possible arrangement.
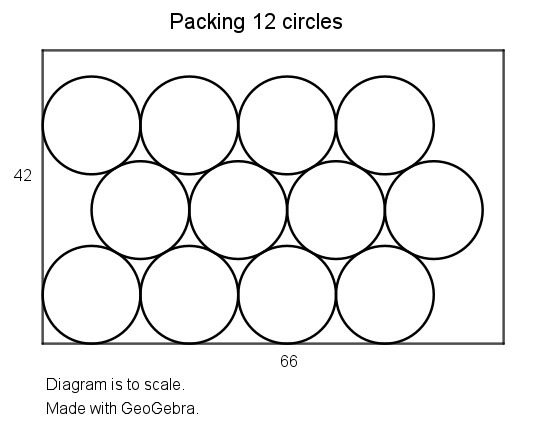
Each row has 4 circles, and there are 3 rows, giving 4*3 = 12 circles.
Can we do better than 12?
Turns out we can.
13 is also possible as shown here:
I imagine each column of circles as snowmen. The bigger snowmen are 3 circles tall. There are 3 of these snowmen, so that's 3*3 = 9 circles so far. The shorter snowmen add in 2*2 = 4 extra circles. That's 9+4 = 13 circles total. An alternative would simply be to count the circles in any fashion you want.
I don't think anything higher than 13 is possible.
However, I am blanking on a proof at the moment.
I used GeoGebra to ensure each diagram is to scale. That helped me determine if I could pack in any extra circles or not.
Doing this with pieces of paper is a recommended old-school method if you aren't familiar with technology. Be sure to carefully measure everything a few times over.
Side note:
Unfortunately tutor MathLover1 is incorrect.
18 is not the answer.
It's not possible to fit 18 circles into this rectangle.
She did not take into account the empty spaces between the circles. If somehow you could melt the circles (or chop them up into very small pieces), then fitting 18 "circles" would be possible. I put that in quotes because after the circles fall to pieces like this, they aren't whole circles anymore.
|
|
|
