Question 1207652: Hi
Jay,Mel and Lynn had 760 stamps. Jay had 8/9 as many as Mel and 6/11 as many as Lynn. If Jay and Lynn shared the stamps equally how many more stamps did Jay have.
Found 3 solutions by Theo, MathTherapy, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this is what i get.
J = the number of stamps jay had.
M = the number of stamps that mel had.
L = the number of stamps that lynn had.
since the total number of stamp is 760, then J + M + L = 760.
jay had 8/9 as many stamps as mel had, and 6/11 as many stamps as lynn had.
equations for that are:
J = 8/9 * M
J = 6/11 * L
from these equations, solve for M and L to get:
M = 9/8 * J
L 11/6 * J
replacing M and L with J in the equation of J + M + L = 760 gets you:
J + 9/8 * J + 11/6 * J = 760
multiply both sides of this equation by 48 to get:
48J + 54J + 88J = 36480.
combine like terms to get:
190J = 36480.
solve for J to get:
J = 192.
when J = 192, .....
M = 9/8 * J gets you M = 216.
L = 11/6 * J gets you L = 352.
the sum is 192 + 216 + 356 which is equal to 760, so this checks out.
you are asked .....
If Jay and Lynn shared the stamps equally how many more stamps did Jay have?
my interpretation of what this means is that, if they added the stamps that Jay and Lynn had and divided them in two, then each would get the same amount.
the total stamps between J and L are 192 + 352 = 544.
divide that by 2 to get 272.
this says that, if they divided the stamps equally between them, each would get 272 stamps.
272 minus 192 = 80.
352 - 272 = 80.
L would have to give 80 stamps to J so that they would both have 272 stamps each.
jay would get 80 more stamps than he originally had.
i think that's your answer.
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Jay,Mel and Lynn had 760 stamps. Jay had 8/9 as many as Mel and 6/11 as many as Lynn. If Jay and Lynn shared the stamps equally how many more stamps did Jay have.
I have ABSOLUTELY no idea who makes up these types of problems. If you read the problem and think about it, you'll
CLEARLY see that the first two sentences are enough to get a UNIQUE solution, so NOTHING ELSE is needed to solve for the number each person has.
Also, "If Jay and Lynn shared the stamps equally how many more stamps did Jay have," doesn't make much sense. But, upon solving for each person's number, whatever is required can be answered.
Let number Jay, Mel and Lynn have be J, M, and L, respectively
Given that Jay, Mel and Lynn have 760 stamps, we get: J + M + L = 760 ------- eq (i)
Also, given that Jay has 8/9 as many as Mel, we get:  ---- eq (ii)
And, given that Jay has 6/11 as many as Lynn, we get: ---- eq (ii)
And, given that Jay has 6/11 as many as Lynn, we get:  --- eq (iii)
J + M + L = 760 ----- eq (i) --- eq (iii)
J + M + L = 760 ----- eq (i)
 ------ Substituting ------ Substituting 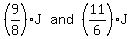 for M and L in eq (i)
24J + 27J + 44J = 24(760) --- Multiplying by LCD, 24
95J = 24(760)
Number of stamps that Jay has, or for M and L in eq (i)
24J + 27J + 44J = 24(760) --- Multiplying by LCD, 24
95J = 24(760)
Number of stamps that Jay has, or  Mel (M) has:
Mel (M) has:  Lynn (L) has:
Lynn (L) has: 
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The information in the first two sentences is enough to determine how many stamps each of them has.
But the question shown in the third sentence is written so badly that we have no idea what the answer is to the question they were trying to ask.
So we can easily find how many stamps each of them has; but, since we don't know what the question is, we can't answer it.
Jay had 8/9 as many stamps as Mel.
J:M = 8:9
Jay had 6/11 as many stamps as Lynn.
J:L = 6:11
Rewrite both of those ratios as equivalent ratios, with the same number for Jay in both ratios.
J:M = 24:27
J:L = 24:44
So now J:M:L = 24:27:44
Let 24x = # of stamps Jay had
then 27x = # Mel had
and 44x = # Lynn had
The total number of stamps was 760:
24x+27x+44x = 760
95x = 760
x = 760/95 = 8
# of stamps Jay had: 24x = 24(8) = 192
# of stamps Mel had: 27x = 27(8) = 216
# of stamps Lynn had: 44x = 44(8) = 352
That's as far as we can go, because we don't know what the question is that we are supposed to answer....
|
|
|