Question 1207307: Hi
Alan has 13 pieces of $2 $5 and $10 notes in his wallet. If the amount of money he has is $67 how many pieces of each note does he have
Found 7 solutions by Edwin McCravy, mccravyedwin, AnlytcPhil, greenestamps, josgarithmetic, ikleyn, MathTherapy:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the numbers of pieces of $2, $5, and $10 notes be, respectively,
x, y, and z.
 Multiply the first equation by -2
Multiply the first equation by -2
 Add the equations term by term:
Add the equations term by term:
 Write all the integers in terms of their nearest multiple of the
smallest absolute value of the coefficients of variables,
which is 3:
Write all the integers in terms of their nearest multiple of the
smallest absolute value of the coefficients of variables,
which is 3:

 Divide thru by 3
Divide thru by 3
 Isolate the fraction terms
Isolate the fraction terms
 The left side is an integer, so the right side must also be an integer,
say A
The left side is an integer, so the right side must also be an integer,
say A
 Multiply the second equation by 3
Multiply the second equation by 3

 Substitute for z in y+3z-14=A:
Substitute for z in y+3z-14=A:



 Substitute for y and z in
Substitute for y and z in



 The general solution in integers is
The general solution in integers is
 x, y, and z must be non-negative integers:
x, y, and z must be non-negative integers:
 => =>  Thus from the above, A can only be 0 or 1
Choose A=0
x=1, y=11, z=1
Choose A=1
x=6, y=3, z=4
Two solutions. [Other choices for A will produce one or more negative answers.]
Edwin
Thus from the above, A can only be 0 or 1
Choose A=0
x=1, y=11, z=1
Choose A=1
x=6, y=3, z=4
Two solutions. [Other choices for A will produce one or more negative answers.]
Edwin
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor shows a solution using formal algebra for the whole problem.
The algebraic part of the solution is much easier if you use some logical reasoning at the beginning.
The total value of the $5 and $10 notes is a multiple of $5; the total value of the 13 notes is $67, which is $2 more than a multiple of $5. So the total value of the $2 notes can only be $2, or $12, or $22, or.... Since the number of notes is 13, the only possibilities are for the total value of the $2 notes to be either $2 or $12.
So treat the problem as two distinct easier problems, using either one or six $2 notes.
(1) Using one $2 note....
The remaining amount, using 12 $5 and $10 notes, is $67-$2=$65. With 12 $5 and $10 notes, the total can be any multiple of $5 between 12($5)=$60 and 12($10)=$120. Since $65 is between $60 and $120, there is a solution using one $2 note.
Use mental arithmetic or formal algebra to find that the solution with one $2 note uses eleven $5 notes and one $10 note.
ANSWER #1: one $2 note, eleven $5 notes, and one $10 note. 1+11+1 = 13; $2+$55+10=$67.
(2) Using six $2 notes....
The remaining amount, using 7 $5 and $10 notes, is $67-$12=$55. With 7 $5 and $10 notes, the total can be any multiple of $5 between 7($5)=$35 and 7($10)=$70. Since $55 is between $35 and $70, there is also a solution using six $2 notes.
Again use mental arithmetic or formal algebra to find that the solution with six $2 notes uses three $5 notes and four $10 notes.
ANSWER #2: six $2 notes, three $5 notes, and four $10 notes. 6+3+4=13; $12+$15+$40=$67.
---------------------------------------------------------------
Added after seeing responses from other tutors....
Responses from other tutors show some form of the equation 8x+3y=41 and then show different ways of finding non-negative integer solutions. Below I show a different way of finding all the solutions, starting from that equation.
In the equation 8x+3y=41, x and y are integers. 8x is even, and 41 is odd, so 3y must be odd; that means y is odd.
To find the "first" solution, use trial and error, using the smallest odd numbers for y, to find the smallest odd y that produces an integer value for x.
y=1: 8x+3=41; 8x=38 --> No...
y=3: 8x+9=41; 8x=32 --> Yes, x=4
So one solution is with y=3 and x=4; then, since x+y+z=13, z=6.
ANSWER #1: (x,y,z) = (4,3,6)
Now to find the other solutions....
The coefficients 8 and 3 in the equation 8x+3y=41 are relatively prime. When that is the case, all other solutions can be found by either adding 3 to x and subtracting 8 from y, or by subtracting 3 from x and adding 8 to y.
Our first solution was with y=3, so we can't subtract 8 from y to get another solution. But we can add 8 to y=3 to get y=11; when we do that, we subtract 3 from x=4 to get x=1. That gives us a second solution. With x=1 and y=11, x+y+z=13 gives us z=1.
ANSWER #2: (x,y,z) = (1,11,1)
We can't find other answers in non-negative integers by that method, so the two solutions we have found are the only ones.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website!
BILL VALUE-FACE VARIABLE MONEY
Ten 10 x 10x
Fove 5 y 5y
Two 2 z 2z
TOTAL 67
And,  , for 13 pieces , for 13 pieces
 , for amount of money. , for amount of money.
Eliminate z, to have a single equation in x and y.

 ---------find some meaningful whole value combinations for x and y. ---------find some meaningful whole value combinations for x and y.


(1,11)
(4,3)
What happens to z for either of those two x & y pair?
Either (1,11,1) or (4,3,6).
How is the money quantity with each of those?
 ----A Match! ----A Match!
-
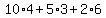 -----also match! -----also match!
RESULT:
One of $10 bill
Eleven of $5 bill
One of $2 bill
Also
four of $10
three of $5
six of $2
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Alan has 13 pieces of $2 $5 and $10 notes in his wallet.
If the amount of money he has is $67 how many pieces of each note does he have ?
~~~~~~~~~~~~~~~~~
In this my post, I'd like to present a regular solution to this problem.
Not the most witty and not the most slow, but something the most REGULAR,
which is in between of these extremes.
Let the numbers of pieces of $2, $5, and $10 notes be, respectively, x, y, and z.
Then you have this system of two equations in three unknowns
x + y + z = 13, (1)
2x + 5y + 10z = 67. (2)
You should find a solution / (solutions) in integer non-negative numbers.
Multiply first equation by 2
2x + 2y + 2z = 26, (1')
2x + 5y + 10z = 67. (2)
Subtract equation (1') from equation (2). You will get
3y + 8z = 41. (3)
This equation is in two unknowns, but you need to solve it in integer non-negative numbers.
Under this restriction, this equation is so called linear Diophantine equation.
A standard way to solve it is "trial and error".
In other words, you should try several integer positive values of z,
and find relevant values of y. Those values of z that provide non-negative integer y will be the solutions.
From equation (3), the candidates for z to try are z = 1, 2, 3, 4, and 5 - - - only five values,
so it is not a catastrophic job to try all five.
To facilitate this job, people usually make a Table such as I provide below
z 41-8z is y = 41-8z Integer solution
a multiple of 3 ? y =  ----------------------------------------------------------------------------
1 41-8*1 = 41- 8 = 33 Yes 11
2 41-8*2 = 41-16 = 25 No
3 41-8*3 = 41-24 = 17 No
4 41-8*4 = 41-32 = 9 Yes 3
5 41-8*5 = 41-40 = 1 No
From the Table, you see that there are exactly two solutions to equation (3) for y and z.
One solution is (y,z) = (11,1). The corresponding value of x, from (1), is x= 13 - y - z = 13 - 11 - 1 = 1.
The other solution is (y,z) = (3,4). The corresponding value of x, from (1), is x= 13 - y - z = 13 - 3 - 4 = 6.
At this point, the problem is just solved, in full.
ANSWER. There are two solutions.
One solution is (one $2 note, eleven $5 notes and one $10 note).
The other solution is (six $2 notes, three $5 notes and four $10 notes).
You can easily CHECK it on your own that these numbers satisfy to all problem's requirements.
----------------------------------------------------------------------------
1 41-8*1 = 41- 8 = 33 Yes 11
2 41-8*2 = 41-16 = 25 No
3 41-8*3 = 41-24 = 17 No
4 41-8*4 = 41-32 = 9 Yes 3
5 41-8*5 = 41-40 = 1 No
From the Table, you see that there are exactly two solutions to equation (3) for y and z.
One solution is (y,z) = (11,1). The corresponding value of x, from (1), is x= 13 - y - z = 13 - 11 - 1 = 1.
The other solution is (y,z) = (3,4). The corresponding value of x, from (1), is x= 13 - y - z = 13 - 3 - 4 = 6.
At this point, the problem is just solved, in full.
ANSWER. There are two solutions.
One solution is (one $2 note, eleven $5 notes and one $10 note).
The other solution is (six $2 notes, three $5 notes and four $10 notes).
You can easily CHECK it on your own that these numbers satisfy to all problem's requirements.
Solved.
-------------------
In this problem, making "trial and errors" was dowable procedure.
In other similar problems, if the number of "trials and errors" is great, you may use
the tools like Excel to facilitate such a job and to make a calculation Table quickly.
In any case, what is described in my post, is traditionally considered as a standard procedure
to solve similar problems.
Again, as a reminder, originally you have only two equations for three unknowns.
But an additional restriction of having non-negative integer solutions reduces
the possible number of solutions from infinity to a finite number.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Alan has 13 pieces of $2 $5 and $10 notes in his wallet. If the amount of money he has is $67 how many pieces of each note does he have
Let number of $2 and $5 notes be T, and F, respectively
Since there are 13 notes, number of $10 notes = 13 - T - F
We then get the total-amount equation as: 2T + 5F + 10(13 - T - F) = 67
2T + 5F + 130 - 10T - 10F = 67
- 8T - 5F = 67 - 130
8T + 5F = 63
Now, as 3 UNKNOWNS/VARIABLES are being sought, but an equation with 2 variables is derived, we use the
DIOPHANTINE-EQUATIION method to solve.
8T + 5F = 63 ----- eq (i)
Because MULTIPLES of 5 have units digits of either 0 or 5, we solve eq (i) in terms of F, so our final
equation will have a denominator of 5
8T + 5F = 63 then becomes:  Now, looking at the above equation, we see that, substituting values of T, from 1, up to 7 - NOT 8,
because 63 - 8(8) will produce a NEGATIVE number of $5 bills (UNACCEPTABLE!!) in the numerator. Now,
again looking at
Now, looking at the above equation, we see that, substituting values of T, from 1, up to 7 - NOT 8,
because 63 - 8(8) will produce a NEGATIVE number of $5 bills (UNACCEPTABLE!!) in the numerator. Now,
again looking at  , we see that the numerator 63 - 8T MUST produce a number that is a
MILTIPLE of 5, but 5's MULTIPLES ONLY end in 0 or 5. Therefore, the numbers from 1 - 7 that MUST be
multiplied by the 8 in 8T, MUST PRODUCE a number that, when SUBTRACTED from 63, gives a MULTIPLE of
5 (the denominator) with units digit of either 0 or 5. For this numerator-MULTPLE of 5 to end
in 0, a MULTIPLE of 8 would need to end with a units digit of 3 (63 - ?3 = ?0). But, there is NO
MULTIPLE of 8 that end in 3. AS a matter of fact, 8 is an even number and when multiplied by any
other number (odd or even), another EVEN number will ensue. So, the only other multiples of 8 would
be those that end in 8 (have a units digit of 8). When checked, digits from 1 - 7, produce only 2
multiples of 8 that end with an 8. These are 1 (8 * 1 = 8), and 6 (8 * 6 = 48). Let's now apply these
values of T to the DIOPHANTINE equation, , we see that the numerator 63 - 8T MUST produce a number that is a
MILTIPLE of 5, but 5's MULTIPLES ONLY end in 0 or 5. Therefore, the numbers from 1 - 7 that MUST be
multiplied by the 8 in 8T, MUST PRODUCE a number that, when SUBTRACTED from 63, gives a MULTIPLE of
5 (the denominator) with units digit of either 0 or 5. For this numerator-MULTPLE of 5 to end
in 0, a MULTIPLE of 8 would need to end with a units digit of 3 (63 - ?3 = ?0). But, there is NO
MULTIPLE of 8 that end in 3. AS a matter of fact, 8 is an even number and when multiplied by any
other number (odd or even), another EVEN number will ensue. So, the only other multiples of 8 would
be those that end in 8 (have a units digit of 8). When checked, digits from 1 - 7, produce only 2
multiples of 8 that end with an 8. These are 1 (8 * 1 = 8), and 6 (8 * 6 = 48). Let's now apply these
values of T to the DIOPHANTINE equation,  With T = 1, we get:
With T = 1, we get:  With T = 6, we get: With T = 6, we get:  Number of $5 notes, or
Number of $5 notes, or  Number of $5 notes, or Number of $5 notes, or  As such, number of $10 notes = 13 - 1 - 11 = 1 As such, number of $10 notes = 13 - 6 - 3 = 4
This gives us:
As such, number of $10 notes = 13 - 1 - 11 = 1 As such, number of $10 notes = 13 - 6 - 3 = 4
This gives us:  This gives us: This gives us: 
|
|
|