SOLUTION: A and B are running a race. A has an 84 feet head start when they begin running. B runs 12 feet while A covers 8 feet. Determine distance A runs before B overtakes A. Not su

Click here to see ALL problems on Miscellaneous Word Problems

Question 1205894: A and B are running a race. A has an 84 feet head start when they begin running.
B runs 12 feet while A covers 8 feet. Determine distance A runs before B overtakes A.
Not sure how to solve.
Found 4 solutions by josgarithmetic, ikleyn, greenestamps, MathTherapy:
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
t, some time unit
Speed for A,
Speed for B,
x, the time for B to close the initial 84 feet distance from A.

, again t is just a time unit; not a variable.

time units B to catchup to A.

Distance A traveled during the catchup time:

Answer by ikleyn(52775)   (Show Source):
You can put this solution on YOUR website!
.
A and B are running a race. A has an 84 feet head start when they begin running.
B runs 12 feet while A covers 8 feet. Determine distance A runs before B overtakes A.
~~~~~~~~~~~~~~~~~~~

Let d be the distance A runs before B overtakes A. Then the distance that B will cover at that time moment is (d+84) feet. Their speeds are in the ratio = = . They spend the same time - THEREFORE, the ratio of distances is the same as the ratio of their speeds. So, we write this proportion = . Cross-multiply 3d = 2*(d+84). Simplify and find d 3d = 2d + 2*84 3d - 2d = 2*84 d = 168. ANSWER. The distance A runs before B overtakes A is 168 feet.

Solved.

---------------

Just fixed my error.
Thanks to @greenestamps !

Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

(Note to tutor @ikleyn: fix a small error in your response....)

The other tutor shows a perfectly good way to set up and solve the problem.

Here is a very different way to set up and solve the problem.

Over some time interval, B runs 12 feet while A runs 8 feet; in that time interval B runs 4 feet farther than A.

A is 84 feet ahead of B at the start; the number of time intervals needed for B to overtake A is 84/4 = 21.

So the distances the two of them run before B overtakes A are:

A: 21*8 = 168 feet
B: 21*12 = 252 feet

ANSWER: (distance A runs before B overtakes him) 168 feet

That same solution formally....

Let x be the number of time intervals in which B runs 12 feet and A runs 8 feet.

12x = distance B runs
8x = distance A runs

In overtaking A, B runs 84 feet farther than A:
12x = 8x+84
4x = 84
x = 21

ANSWER: the distance A runs is 8x = 168 feet

Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!

A and B are running a race. A has an 84 feet head start when they begin running. B runs 12 feet while A covers 8 feet. Determine distance A runs before B overtakes A. Not sure how to solve. Let distance A travels before being overtaken by B, be D Since A is already 84 feet ahead of B, then distance B travels to overtake A = "D + 84" feet Since B's speed is 12 feet, per time period, B's time to get to "catch-up" point = 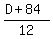Also, since A's speed is 8 feet, per time period, A's time to get to "catch-up" point = 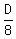Because the time they take to get to the catch-up point is the same, we get: 2(D + 84) = 3D ----- Multiplying by LCD, 24 2D + 2(84) = 3D 2(84) = 3D - 2D Distance A travels before being overtaken by B, or