SOLUTION: Hi Jerry drove from A to B at 64km per hour. Two hours after Jerry started driving harry started driving from B to A at 96km per hour. When Jerry reached B harry was still 32km fr

Let d be the unknown distance between A and B, in kilometers,
and let t be the time Harry drove before he met Jerry.


Then we can write the full distance equation between A and B in the form

    64(t+2) + 96t = d.    (1)


Thus we have one equation for two unknowns, and we, obviously, need a second equation.

I am going to write this equation by equating the time Jerry spent drown from the meeting point to B,
and the time Harry spent from the meeting point to the point 32 km before A.


The distance from the meeting point to B is 96t kilometers;
So, Jerry spent 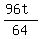 hours to get B from the meeting point.


The distance from the meeting point to A is 64*(t+2) km.  From it, I should subtract 32 km.
So, when Jerry reached A, Harry covered 64(t+2)-32 kilometers from the meeting point.


Therefore, the "time equation" is

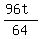     = .    (2)


Left side is the Jerry's time; right side is the Harry's time.


Now we have two equations, (1) and (2), for two unknowns.
Thus, we completed the setup and are ready now to solve this system.  


Simplify equation (2) step by step

     = 

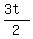    9t = 2*(2(t+2)-1)

    9t = 2*(2t+3)

    9t = 4t + 6

    9t - 4t = 6

       5t   = 6

        t   = 6/5  of an hour, or 1.2 of an hour.


Now substitute t = 1.2 into equation (1) and find the distance

    d = 64*(1.2+2) + 96*1.2 = 320 kilometers.


ANSWER.  The distance between A and B is 320 kilometers.