Question 1204434: On a wall 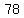  cm wide, Peter is going to hang five pictures beside each other, each measuring cm wide, Peter is going to hang five pictures beside each other, each measuring   cm wide. He will leave cm wide. He will leave   cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture and will centre these nails leaving cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture and will centre these nails leaving   cm between each pair. How far, in cm, from the end of the wall (on either side) will the first nail be placed? cm between each pair. How far, in cm, from the end of the wall (on either side) will the first nail be placed?
Found 2 solutions by math_tutor2020, MathTherapy:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll convert each of the given mixed numbers into decimal form
78 & 2/5 = 78.4
12 & 1/2 = 12.5
2 & 3/5 = 2.6
4 & 1/2 = 4.5
Each result is exact.
Draw out a horizontal number line. Let's say the number line starts at x = 0 and ends at x = 78.4 to represent the width of the wall.
Don't worry about the diagram being to scale or not.
One picture takes up 12.5 cm of horizontal space along this number line.
Five pictures of the same width take up 5*12.5 = 62.5 cm
Add in the four gaps between neighboring pictures and we add another 4*2.6 = 10.4 cm
So far 62.5+10.4 = 72.9 cm is accounted for.
I'll assume that Peter is hanging the pictures so that they are symmetrically spaced between each opposite wall.
If so then let k be the distance from the wall's edge to the first picture near that wall. It also represents the buffer distance from the other wall to the last picture.
We add 2 copies of k onto the 72.9 and set it equal to 78.4 so we can solve for k.
k+72.9+k = 78.4
2k+72.9 = 78.4
2k = 78.4-72.9
2k = 5.5
k = 2.75
Let's say we started at the left wall.
Move 2.75 cm to the right to arrive at the left edge of the first picture.
Move another (12.5)/2 = 6.25 cm to the right to arrive at the x coordinate of the center of the 1st picture.
Move left (4.5)/2 = 2.25 cm so that we can locate the x coordinate of the first nail.
This places us at the x coordinate 2.75 + 6.25 - 2.25 = 6.75
Answer: 6.75 cm
This converts to the mixed number 6 & 3/4 or we can write it as 
Edit: Tutor MathTherapy arrived at a different answer because he interpreted the problem differently than I did.
Consider labeling the first four nails as A,B,C,D
My interpretation is that distance(A,B) = 4.5 cm while MathTherapy's interpretation is distance(B,C) = 4.5
Upon closer inspection, both interpretations seem valid. The wording "leaving 4.5 cm between each pair" is a bit vague.
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
On a wall 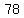  cm wide, Peter is going to hang five pictures beside each other, each measuring cm wide, Peter is going to hang five pictures beside each other, each measuring   cm wide. He will leave cm wide. He will leave   cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture and will centre these nails leaving cm in between each pair of adjacent pictures. He plans to use two nails to hang each picture and will centre these nails leaving   cm between each pair. How far, in cm, from the end of the wall (on either side) will the first nail be placed?
I think a diagram is in order, so this can be better understood. cm between each pair. How far, in cm, from the end of the wall (on either side) will the first nail be placed?
I think a diagram is in order, so this can be better understood.  .
I'll keep every measurement in fractional-form, to make it easy for ME to provide an answer
As there are 5 pictures, there will be 5 - 1 or 4 spaces between the pics.
With space between each pic. being .
I'll keep every measurement in fractional-form, to make it easy for ME to provide an answer
As there are 5 pictures, there will be 5 - 1 or 4 spaces between the pics.
With space between each pic. being 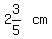 , total space between the 5 pics. is, , total space between the 5 pics. is,  Total space for the 5 pics:
Total space for the 5 pics:  Total horizontal-space occupied by the 5 pics., separated by
Total horizontal-space occupied by the 5 pics., separated by 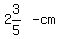 spaces: spaces:  Total space REMAINING in the allotted
Total space REMAINING in the allotted 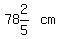 space: space:  Space to the RIGHT of the left-side of the wall where the 1st of the 5 pics should be placed:
Space to the RIGHT of the left-side of the wall where the 1st of the 5 pics should be placed:  . This is also the space to the LEFT of the right-side of the wall where the 5th
or last of the 5 pics, should be placed.
Now, it would be a good time to check to see if ALL . This is also the space to the LEFT of the right-side of the wall where the 5th
or last of the 5 pics, should be placed.
Now, it would be a good time to check to see if ALL 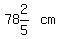 of space will be occupied. For this,
we get: of space will be occupied. For this,
we get:  . This CHECKS!!
From what I understand, 2 nails will be used to hang each pic, and the 2 nails will be CENTERED behind each pic.,
so that each pair of nails - behind each pic. - will be . This CHECKS!!
From what I understand, 2 nails will be used to hang each pic, and the 2 nails will be CENTERED behind each pic.,
so that each pair of nails - behind each pic. - will be  from each preceding and each succeeding pair of nails.
This means that the space between the 2nd of the 1st pair of nails and the 1st nail of the 2nd pair will be from each preceding and each succeeding pair of nails.
This means that the space between the 2nd of the 1st pair of nails and the 1st nail of the 2nd pair will be  apart.
With space between pics. being apart.
With space between pics. being 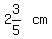 , remaining space between each pair of nails = , remaining space between each pair of nails =  Therefore, space on EITHER side of the space between each pic. =
Therefore, space on EITHER side of the space between each pic. =  Finally, the 1st nail should be placed
Finally, the 1st nail should be placed  to the right of the to the right of the  point from the left-side of the wall, or point from the left-side of the wall, or  from the left side of the wall. This is the same for the right-side of the wall, also!!
All/Most of this might be confusing, but should be much clearer after the above diagram is viewed. from the left side of the wall. This is the same for the right-side of the wall, also!!
All/Most of this might be confusing, but should be much clearer after the above diagram is viewed.
|
|
|