Question 1203641: Hi
In a fish tank there were 35 more guppies than goldfish. When more guppies and goldfish were added the number of guppies increased by 1/6 and the number of goldfish by 3/5 . Then the total number of fish in the tank was 193. How many guppies were there in the end.
Thanks
Found 5 solutions by Edwin McCravy, ankor@dixie-net.com, Theo, josgarithmetic, ikleyn:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! g = number of guppies
f = number of goldfish
g = f + 35
g + 1/6 * g + f + 3/5 * f = 193
simplify to get:
7/6 * g + 8/5 * f = 193
you are given that g = f + 35
replace g in the equation of 7/6 * g + 8/5 * f = 193 with f + 35 to get:
7/6 * (f + 35) + 8/5 * f = 193
simplify to get:
7/6 * f + 7/6 * 35 + 8/5 * f = 193
multiply both sides of the equation by 30 to get:
35 * f + 35 * 35 + 48 * f = 193 * 30
simplify to get:
35 * f + 1225 + 48 * f = 5790
combine like terms to get:
83 * f + 1225 = 5790
subtract 1225 from both sides of the equation to get:
83 * f = 4565
solve for f to get:
f = 55
since g = f + 35, then you get:
f = 55
g = 90
confirm by replacing g and f in the original equations to get:
g = f + 35 becomes 90 = 55 + 35 which becomes 90 = 90.
this confirmns that g = f + 35 is true.
g + 1/6 * g + f + 3/5 * f = 193 becomes:
90 + 1/6 * 90 + 55 + 3/5 * 55 = 193 which becomes:
105 + 88 = 193 which becomes 193 = 193.
this confirms that g + 1/6 * g + f + 3/5 * f is true.
your solution is that there were 105 guppies in the end.
that would be 90 guppies to start plus 1/6 * 90 = 15 guppies for a total of 105 guppies in the end.
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52905)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is quite obvious that two unknowns are enough to solve the problem.
Two tutors, @ankor@dixie-net.com and @Theo proved it by providing complete solutions
using two variables.
Then suddenly @josgarithmetic comes with his idea to use 4 unknowns,
and writes the system of three equations for it, proposing the student to use it.
Obviously, this his idea is not very smart (if do not say more).
Also, it is obvious that it is NOT POSSIBLE to find 4 unknowns from the system of three equations.
Therefore, my advise to the reader is to ignore the post by @josgarithmetic,
as if you've never seen it - for safety of your mind.
Below is my solution using only one unknown.
Let x be the number of goldfish, initially.
Then the number of guppies was (x+35), initially.
Adter adding, there are 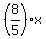 of goldfish and of goldfish and 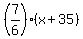 of guppies.
The total is 193 now of guppies.
The total is 193 now
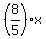 + + 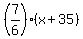 = 193.
To solve this equation, multiply the terms by 30. You will get
48x + 35(x+35) = 30*193.
Simplify it further
48x + 35x = 30*193 - 35*35
83x = 4565
x = 4565/83 = 55.
So, initially there were 55 goldfish in the tank and (55+35) = 90 guppies.
At the end, there is = 193.
To solve this equation, multiply the terms by 30. You will get
48x + 35(x+35) = 30*193.
Simplify it further
48x + 35x = 30*193 - 35*35
83x = 4565
x = 4565/83 = 55.
So, initially there were 55 goldfish in the tank and (55+35) = 90 guppies.
At the end, there is 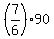 = 105 guppies in the tank.
ANSWER. There are 105 guppies in the tank at the end. = 105 guppies in the tank.
ANSWER. There are 105 guppies in the tank at the end.
Solved.
|
|
|