Question 1201597: Radioactive Carbon-14,which is found in all living things, has a half-life of 5700 years and can be used to date fossils. Suppose a fossil contains 15% of the amount of Carbon-14 that the organism contained when it was alive. Calculate the age of the fossil.
Found 4 solutions by Theo, math_tutor2020, josgarithmetic, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the half life is 5700.
equation for that is 1/2 = (1 + r) ^ 5700
solve for (1 + r) to get (1 + r) = (1/2) ^ (1/5700) = .9998784026.
that's the growth factor per year.
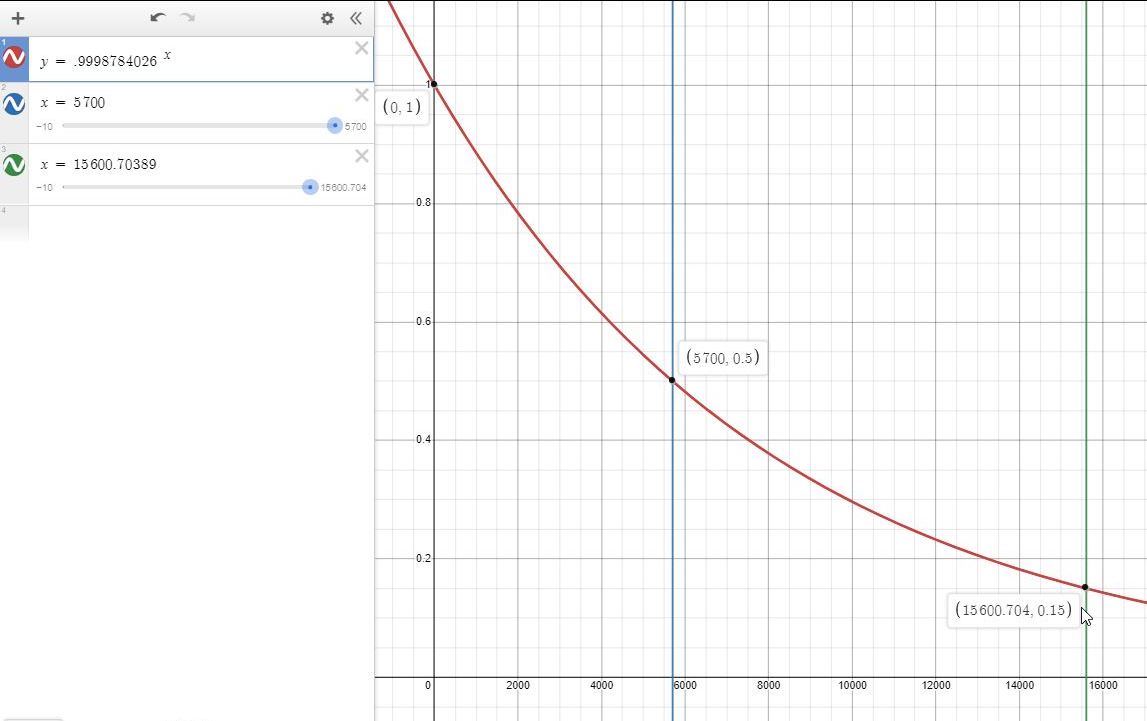
in 5700 years, a present value of 1 is equal to .9998784026 ^ 5700 = .5
if a fossil contains 15% of the carbon-14 that it contained when it was alive, the formmula becomes:
.15 = .9998784026 ^ x
take the log of both sides of the equation to get:
log(.15) = log(.9998784016 ^ x)
this becomes log(.15) = x * log(.9998784026)
solve for x to get x = log(.15) / log(.9998784026) = 15600.70389.
the age of the fossil is 15600.70389 years.
the equation can be graphed as y = .9998784026 ^ x, as shown below.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 15600 years old (approximate)
Work Shown:
a = starting amount = doesn't matter since it cancels out later
0.15a = 15% of the starting amount
x = number of years
y = amount of material remaining
H = 5700 = half-life
Half-life formula
y = a*(0.5)^(x/H)
0.15a = a*(0.5)^(x/5700)
0.15 = (0.5)^(x/5700)
Log(0.15) = Log( (0.5)^(x/5700) )
Log(0.15) = (x/5700)*Log(0.5)
x/5700 = Log(0.15)/Log(0.5)
x = 5700*Log(0.15)/Log(0.5)
x = 15600.7038867473
x = 15600
The substance is roughly 15600 years old.
Round this however your teacher instructs.
I decided to round to the nearest hundred.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Radioactive Carbon-14, which is found in all living things, has a half-life of 5700 years
and can be used to date fossils. Suppose a fossil contains 15% of the amount of Carbon-14
that the organism contained when it was alive. Calculate the age of the fossil.
~~~~~~~~~~~~~~~~~~~~~~~~
From the condition, you see that half-life period is given of 5700 years.
As soon as you see it, you write the exponential decay function with the base  in the form
m(t) =
in the form
m(t) = 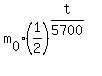 . (1)
Here m(t) is the current mass of the radioactive Carbon-14; . (1)
Here m(t) is the current mass of the radioactive Carbon-14; 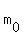 is its initial mass;
t is the time after this organism died.
Notice that the degree at is its initial mass;
t is the time after this organism died.
Notice that the degree at  is the ratio of the current time to the given half-time.
+------------------------------------------------+
| So, it is good start and it is RIGHT start. |
+------------------------------------------------+
Next, you are given the ratio is the ratio of the current time to the given half-time.
+------------------------------------------------+
| So, it is good start and it is RIGHT start. |
+------------------------------------------------+
Next, you are given the ratio 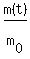 ; so, you divide equation (1) by ; so, you divide equation (1) by 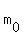 ,
and you get ,
and you get
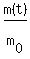 = =  .
The ratio .
The ratio 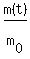 is given in the problem: it is 0.15; so, your equation takes the form
0.15 = is given in the problem: it is 0.15; so, your equation takes the form
0.15 =  . (2)
You should solve this exponential equation and find "t" from it.
To solve it, take logarithm base 10 of both sides. Using standard properties of logarithms, you get
log(0.15) = . (2)
You should solve this exponential equation and find "t" from it.
To solve it, take logarithm base 10 of both sides. Using standard properties of logarithms, you get
log(0.15) = 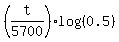 .
It gives you
t = .
It gives you
t = 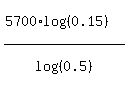 = 15600.7 years.
In carbon dating problem, it is commonly accepted to round the final computed age to closest hundreds of years.
So, your answer is 15600 years. = 15600.7 years.
In carbon dating problem, it is commonly accepted to round the final computed age to closest hundreds of years.
So, your answer is 15600 years.
Solved.
-------------------
What is written in my post, is a standard mantra for this kind of problems.
There is a group of lessons in this site, which covers many similar problems on Carbon dating
- Using logarithms to solve real world problems
- Radioactive decay problems
- Carbon dating problems
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
///////////////////
Regarding two other posts, I'd like to make couple notices.
To present a solution in a way how @Theo makes in his post, is WRONG way teaching,
because under given conditions, when half-life is given, there is no need to use ekt-form of exponential function, AT ALL.
THEREFORE, to teach as @Theo does in his post, is the same as to teach playing chess game by making obviously wrong first move.
To solve as @josgarithmetic does in his post, is obviously wrong way to teach beginning students.
It is so obvious that does not require any explanations.
Thanks to god, nobody in healthy mind teaches this way.
|
|
|