Question 1201553: The radioactive isotope of potassium-42, which is vital in the diagnosis of brain tumors, has a half life of 12.36 hours.
How long will it take for the original 500 mg sample to decay to a mass of 5 mg?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39614)   (Show Source): (Show Source):
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The radioactive isotope of potassium-42, which is vital in the diagnosis of brain tumors,
has a half life of 12.36 hours.
How long will it take for the original 500 mg sample to decay to a mass of 5 mg?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Since you are given the half-life time period of 12.36 hours,
use the standard exponential decay formula with the base (1/2)
m(t) = 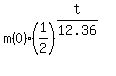 , (1)
where m(0) is the starting mass at t= 0 and m(t) is remaining mass in the current time moment t,
t is the time in hours.
Substitute the given data into equation (1)
5 = , (1)
where m(0) is the starting mass at t= 0 and m(t) is remaining mass in the current time moment t,
t is the time in hours.
Substitute the given data into equation (1)
5 =  .
It is your equation to solve in order for find t.
To solve it, first divide both sides by 500. You will get .
It is your equation to solve in order for find t.
To solve it, first divide both sides by 500. You will get
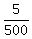 = = 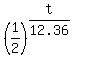 , or 0.01 = , or 0.01 =  .
Next, take logarithm base 10 of both sides
log(0.01) = .
Next, take logarithm base 10 of both sides
log(0.01) = 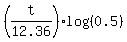 ,
which gives you
t = ,
which gives you
t =  = use your calculator = 82.1181 hours (rounded). ANSWER = use your calculator = 82.1181 hours (rounded). ANSWER
Solved, with all necessary explanations.
-----------------
On radioactive decay, see the lesson
- Radioactive decay problems
in this site.
You will find many similar (and different) solved problems there.
Use this lesson as your handbook, textbook, guide, tutorials, and (free of charge) home teacher.
Learn the subject from there once and for all.
////////////////////
The major reason, why I started write this my post, is to teach you that in radio-active decay problems,
when the half-life is given, you should use the exponential decay model with the base 1/2,
which leads you to the end and to the answer by a SHORTEST way.
It is not only the SHORTEST way in such problems, but it is the EXPECTED way, too.
Finally, it is not only the shortest way and not only the expected way:
it is a GOOD STYLE way, which demonstrates
that you do understand the subject in full and PRECISELY as it is.
|
|
|