SOLUTION: At time=0, there are 6,000 grams of a radioactive material present. The half-life of the element is 18 years. In how many years will there be 115 grams remaining? Round your answer

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: At time=0, there are 6,000 grams of a radioactive material present. The half-life of the element is 18 years. In how many years will there be 115 grams remaining? Round your answer      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1201501: At time=0, there are 6,000 grams of a radioactive material present. The half-life of the element is 18 years. In how many years will there be 115 grams remaining? Round your answer to the nearest 0.01 years.
Any help would be appreciated, I have tried many problems like this one without success.
Found 3 solutions by math_tutor2020, josgarithmetic, MathTherapy:
Answer by math_tutor2020(3816) About Me  (Show Source):
You can put this solution on YOUR website!

Answer: 102.69 years

Work Shown:

x = number of years
y = amount of substance leftover, in grams

One possible equation is
y = 6000*(0.5)^(x/18)
it is of the format
y = a*(0.5)^(x/H)
where 'a' is the starting amount and H is the half-life in years.

Plug in y = 115 and solve for x.
We'll need to use logs to isolate the exponent.
If the variable is in the trees, then we log it down.

y = 6000*(0.5)^(x/18)
115 = 6000*(0.5)^(x/18)
115/6000 = (0.5)^(x/18)
0.0191667 = (0.5)^(x/18)
Log(0.0191667) = Log( (0.5)^(x/18) )
Log(0.0191667) = (x/18)*Log( 0.5 ) ... use the logarithm power rule
x/18 = Log(0.0191667)/Log( 0.5 )
x = 18*Log(0.0191667)/Log( 0.5 )
x = 102.694576057311
x = 102.69
It takes roughly 102.69 years to have 115 grams of substance remaining.


Another problem involving half-life.
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1201494.html

Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
y=p%281%2F2%29%5E%28x%2Fh%29
p, initial amount
h, half life
x, amount time passage
y, amount after x time

log%28%28y%29%29=log%28%28p%29%29%2Blog%28%28%281%2F2%29%5E%28x%2Fh%29%29%29
log%28%28y%29%29=log%28%28p%29%29%2B%28x%2Fh%29log%28%281%2F2%29%29
log%28%28y%29%29-log%28%28p%29%29=%28x%2Fh%29%28-log%28%282%29%29%29
log%28%28p%29%29-log%28%28y%29%29=%28x%2Fh%29log%28%282%29%29
log%28%28p%2Fy%29%29%28h%2Flog%28%282%29%29%29=x
highlight%28x=%28h%2Flog%28%282%29%29%29log%28%28p%2Fy%29%29%29
Your values to substitute are
system%28h=18%2Cy=115%2Cp=6000%29

Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!
At time=0, there are 6,000 grams of a radioactive material present. The half-life of the element is 18 years. In how many years will there be 115 grams remaining? Round your answer to the nearest 0.01 years.

Any help would be appreciated, I have tried many problems like this one without success. 

If ½-life is “a” time-periods, then k, or DECAY CONSTANT = 

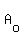CONTINUOUS GROWTH/DECAY formula: matrix%281%2C3%2C+A%2C+%22=%22%2C+A%5Bo%5De%5E%28kt%29%29, with:
A  being remaining amount after time t (115, in this case)
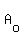A%5Bo%5D being Original/Initial amount (6,000, in this case)
k  being the constant (k > 0 signifies RATE OF GROWTH ;  k < 0 signifies RATE OF DECAY ; k = - .0385, in this case) 
t  being time, in stated periods (Unknown, in this case)

                                          matrix%281%2C3%2C+A%2C+%22=%22%2C+A%5Bo%5De%5E%28kt%29%29
                                        matrix%281%2C3%2C+115%2C+%22=%22%2C+%226%2C000%22e%5E%28-+.0385t%29%29 ----- Substituting 115 for A, 6,000 for A%5Bo%5D, and - .0385 for k
                                      
                                   matrix%281%2C3%2C+-+.0385t%2C+%22=%22%2C+ln+%2823%2F%221%2C200%22%29%29 ------ Converting to LOGARITHMIC (Natural) form
Time it takes for 115 grams to remain, or 

The correct answer should actually be in WHOLE-NUMBER years (103 to be specific)!