Question 1201461: At time t=0, a cup of coffee at 187*d F is placed in a room at 72*d F. After t=4 minutes, the coffee has cooled to a temp of 160*d F. In how many minutes will the coffee reach 130*d F? Round your answer to the nearest 0.01 minutes.
Any and all help on this problem will be greatly appreciated :)
Answer by ikleyn(52767)   (Show Source):
You can put this solution on YOUR website! .
At time t=0, a cup of coffee at 187*d F is placed in a room at 72*d F.
After t=4 minutes, the coffee has cooled to a temp of 160*d F.
In how many minutes will the coffee reach 130*d F? Round your answer to the nearest 0.01 minutes.
Any and all help on this problem will be greatly appreciated :)
~~~~~~~~~~~~~~~~~~
The Newton law of cooling states that the temperature of the cup of coffee in the room is this function of time t
T(t) =  =  .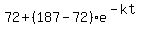
where "k" is the decay constant.
At t= 4 minutes T(t)= 160, which gives you an equation to find the decay constant k:
160 = 72 + 115*e^(-k*4),
115*e^(-k*4) = 160 - 72 = 88,
e^(-4k) =  = 0.765217.
Take natural logarithms of both sides
-4k = ln(0.765217)
k =  = 0.0669.
+------------------------------------------+
| Thus the decay constant k is found. |
+------------------------------------------+
The next and last step is to find the time under the question.
For it, you have this (the same) Newton's cooling equation
T(t) =  = 130,
e(-0.0669*t) = 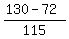 = 0.50435.
Take natural logarithm of both sides
-0.0669*t = ln(0.50435)
and find
t =  = 10.23 minutes (rounded as requested).
Answer. 10.23 minutes counting from the very beginning time moment.
Solved.
-------------------
So, the problem is solved in two steps.
In the first step, we find the decay coefficient of the cooling equation, using first portion of the given data.
In the second step, we find the time getting the given temperature, using the found value of the decay coefficient.
To see many other similar (and different) solved problems of this type, look into the lesson
- Solving problem on Newton Law of cooling
in this site.
Learn the subject from there.
|
|
|
