Question 1201382: Hi
The ratio of 20cent coins and 10cent coins was 4:7 respectively. After exchanging 8 20cent coins for 10cent coins the ratio became 2:11 . How much money did Bob have at first.
Thanks
Found 3 solutions by ikleyn, Theo, greenestamps:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
The ratio of 20cent coins and 10cent coins was 4:7 respectively.
After exchanging 8 20cent coins for 10cent coins the ratio became 2:11 .
How much money did Bob have at first.
~~~~~~~~~~~~~~~~
At first, there were 4x 20-cent coins and 7x 10-cent coins.
After exchange 8 20-cent coins for 10-cent coins, there were
(4x-8) 20-cent coins and (7x+16) 10-cent coins.
Your equation is
 =  .
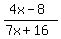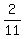Solve and find x
11*(4x-8) = 2*(7x+16)
44x - 88 = 14x + 32
44x-14x = 32 + 88
30x = 120
x = 120/30 = 4.
At first, there were 20*4x + 10*7x = 80x + 70x = 150x = 150*4 = 600 cents = 6 dollars. ANSWER
Solved.
////////////////
It is a standard style which @Theo uses in solving Algebra problems and presenting his solutions:
he takes the most inappropriate approach and writes a solution in 3-5 times longer than it should be.
He repeats it every day, from month to month.
As soon as he sees my short solution, he considers it as his duty to write his own solution in 3 - 5 times longer.
I can not imagine a person in healthy mind who will read such solutions.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! x = the number of 20 cent coins.
y = the number of 10 cent coins.
ratio of 20 cent coins to 10 cent coins is 4/7.
you get:
x/y = 4/7
after exchanging 8 twenty cent coins for ten cent coins, the ration becomes 2/11.
8 twenty cent coins is equal to 16 ten cent coins.
you get:
(x-8)/(y+16) = 2/11
in tyhe second equation, cross multiply to get:
(x-8)*11 = (y+16)*2
simplify to get:
11x-88 = 2y+32
since x/y = 4/7, solve for x to get:
x = 4y/7
replace x in the equation of 11x-88 = 2y+32 to get:
11*4y/7 - 88 = 2y + 32
simplify to get:
44y/7 - 88 = 2y + 32
add 88 to both sides of the equation to get:
44y/7 = 2y+120
multiply both sides of the equation by 7 to get:
44y = 14y + 840
subtract 14y from both sides of the equation to get:
30y = 840
solve for y to get:
y = 840/30 = 28
from the original equation of x/y = 4/7, rplace y with 28 to get:
x/28 = 4/7
multiply both sides of this equation by 28 to get:
x = 28*4/7 = 16
you have:
x = 16
y = 28
x/y = 16/28 = 4/7
(x-8)/(y+16) = 8/44 = 2/11
looks like the value of x = 16 and y = 28 are good.
they wanted to know how much money bob had at first.
at first he had 16 twenty cent coins and 28 ten cent coins.
the value would be 16 * .20 + 28 * .10 = 3.20 + 2.80 = 6.00
after he exchanged the coins, he should have the same amount, if i understood your problem correctly.
after the exchange, he had 8 twenty cent coins and 44 ten cent coins.
8 * .20 + 44 * .10 = 1.60 + 4.40 = 6.00, confirming that this is true.
your solution, as best i can determine, is he has $6.00 before and after the exchange.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
A general comment on this kind of problem -- as demonstrated by the two responses you have received to now.
Given a ratio of 4:7, you can let the two numbers be x and y and then solve the problem using two variables and a bunch of operations involving ugly fractions, as one tutor did.
Or you can take the given ratio of 4:7 and let the two numbers be 4x and 7x -- leading to a solution using one variable and very simple operations.
The lesson:
Given a ratio A:B at the beginning of a problem, let the two numbers be Ax and Bx. Virtually always (if not always) that will make solving the problem much easier.
|
|
|
