Question 1201362: Hi
Ali had 60% of the total number of marbles his other 3 friends had. Cindy had 50% of the total number Ben and Daniel had. The number Ben had was 1/3 the number daniel had. If ali had 39 more marbles than daniel, how many did they have altogether. Thanks
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website! This might not be the best way to handle the description, but .... you have three equations and three unknown variables.
Ali (3/5)(c+b+d)
Cindy c=(1/2)(b+d)
Ben b=(1/3)d
Daniel d
(3/5)(c+b+d)=d+39
(Not showing the arithmetic or algebra steps....)
Ali, (3/5)(130+65+195)
Cindy, 130
Ben, 65
Daniel, 195
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
(1) Ali had 60% of the total number of marbles his other 3 friends had.
(2) Cindy had 50% of the total number Ben and Daniel had.
(3) The number Ben had was 1/3 the number daniel had.
(4) If ali had 39 more marbles than daniel, how many did they have altogether.
~~~~~~~~~~~~~~~~~~
For convenience of referencing, I numbered the statements (1), (2), (3) and (4).
Let x be the number of marbles Ben had.
Then from (3), Daniel had 3x marbles,
and Ben and Daniel had together x+3x = 4x marbles.
Then from (2), Cindy had 0.5*(4x) = 2x marbles,
and 3 friends, Ben, Cindy and Daniel, had together 4x+2x = 6x marbles.
Then from (1), Ali had 0.6*(6x) = 3.6x marbles.
We are given in (4), that
3.6x - 3x = 39.
It gives us
0.6x = 39, x = 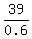 = 65.
Hence, altogether they had 6x+3.6x = 9.6x = 9.6*65 = 624 marbles. ANSWER
Solved using one unknown and one equation.
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website!
Hi
Ali had 60% of the total number of marbles his other 3 friends had. Cindy had 50% of the total number Ben and Daniel had. The number Ben had was 1/3 the number daniel had. If ali had 39 more marbles than daniel, how many did they have altogether. Thanks
Let number Ben has, be B
Since Ben has  Daniel's amount, Daniel then has thrice Ben's, or 3B
Cindy has  of Ben and Daniel's total, and with Ben and Daniel having 4B (B + 3B), Cindy then has: 
Finally, it's said that Ali has 60% of all 3's total, or .6(Ben's + Cindy's + Daniel's), or .6(B + 2B + 3B) = .6(6B) = 3.6B
It's also said that Ali has 39 more than Daniel, or 3B + 39
Therefore, we get: 3.6B = 3B + 39
3.6B - 3B = 39
.6B = 39
Number Ben has, or 
Total: A + B + C + D, or
3.6B + B + 2B + 3B = 9.6B
Total number of marbles:
OR
 OR 
You think you can add them up?
|
|
|
