Question 1201263: Hi
John and Kevin travel from home to school using the same route. They started at the same time. John travelled at 18km per hour. Both did not change their speeds throughout the trip. When Kevin covered 1/4 of the journey, John was 3.5km ahead of him. If John reached school at 9.35am what time did Kevin reach school.
Thanks
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
John and Kevin travel from home to school using the same route.
They started at the same time. John travelled at 18km per hour.
Both did not change their speeds throughout the trip.
When Kevin covered 1/4 of the journey, John was 3.5km ahead of him.
If John reached school at 9.35am what time did Kevin reach school.
~~~~~~~~~~~~~~~~~~
Let x be the distance from home to the school, in kilometers;
Let J be the John' speed, in km/h; let K be the Kevin' speed.
Let' start our clock when both John and Kevin left their home.
From the condition, we can write this equation
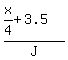 = = 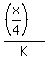 ,
saying that "When Kevin covered 1/4 of the journey, John was 3.5km ahead of him."
We know that J = 18 km/h, so we replace J in this equation by 18. We get then ,
saying that "When Kevin covered 1/4 of the journey, John was 3.5km ahead of him."
We know that J = 18 km/h, so we replace J in this equation by 18. We get then
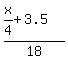 = = 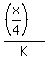 .
Multiply both sides by 4. You will get .
Multiply both sides by 4. You will get
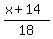 = =  .
The time .
The time  is the time of Kevin's travel and is the time under the problem's question.
The time is the time of Kevin's travel and is the time under the problem's question.
The time 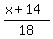 is is 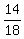 = =  of an hour more than of an hour more than 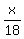 ,
which is the time when John arrived to the school, i.e. 9:35 am. ,
which is the time when John arrived to the school, i.e. 9:35 am.
 of an hour is of an hour is 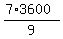 seconds = 7*400 seconds = 2800 seconds = 46 minutes and 40 seconds.
Hence, Kevin reaches the school 46 minutes and 40 seconds after 9:35 am.
ANSWER. Kevin reaches the school at 10:21 minutes and 40 seconds A.M. seconds = 7*400 seconds = 2800 seconds = 46 minutes and 40 seconds.
Hence, Kevin reaches the school 46 minutes and 40 seconds after 9:35 am.
ANSWER. Kevin reaches the school at 10:21 minutes and 40 seconds A.M.
Solved.
/////////////////
It can be re-told in other words.
One can say that under the given condition
"when Kevin covered 1/4 of the journey, John was 3.5km ahead of him"
we have this logical implication
"when Kevin covers the entire journey, John is 4*3.5 km = 14 kilometers ahead of him."
Hence, Kevin reaches the school in that additional time after 9:35 am,
when John covers 14 kilometers, moving at the rate of 18 km/h.
It leads you to the same answer.
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
|
|
|