Question 1196965: Lookouts on two naval vessels, about 2 miles apart, spot a disabled boat off the port side. One lookout spots the boat at an angle of 42° with the line connecting the naval vessels. The other lookout spots the boat at an angle of 28° with the same line.
a. Which naval vessel is closer to the boat?
b. How much closer it?
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Lookouts on two naval vessels, about 2 miles apart, spot a disabled boat off the port side.
One lookout spots the boat at an angle of 42° with the line connecting the naval vessels.
The other lookout spots the boat at an angle of 28° with the same line.
(a) Which naval vessel is closer to the boat?
(b) How much closer it?
~~~~~~~~~~~~~
You have a triangle ABC, where A is the point of the first lookout and B is the point
of the second lookout. The point C is where the disable boat is located.
Answer to (a) is easy: in any triangle, the longer the side is, the greater is the opposite angle.
In our case, angle at A is 42°, while angle at B is 28°.
Since angle A is greater than angle B, it means that side BC is longer than side AB.
Thus, vessel A is closer to the disable boat than vessel B. It is the ANSWER to question (a)
To solve (b), use the sine law
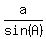 = = 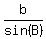 = = 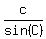 .
We know c = 2 kilometers, C = 180° - 42° - 28 = 110°.
So, .
We know c = 2 kilometers, C = 180° - 42° - 28 = 110°.
So, 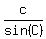 = = 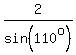 = = 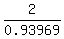 = 2.12836 (rounded).
Therefore, a = 2.12836*sin(A) = 2.12836*sin(42°) = 2.12836*0.66913 = 1.424 kilometers,
b = 2.12836*sin(B) = 2.12836*sin(28°) = 2.12836*0.46947 = 0.999 kilometers.
Thus A is closer than B by a - b = 1.424 - 0.999 = 0.425 kilometers = 425 meters, approximately. = 2.12836 (rounded).
Therefore, a = 2.12836*sin(A) = 2.12836*sin(42°) = 2.12836*0.66913 = 1.424 kilometers,
b = 2.12836*sin(B) = 2.12836*sin(28°) = 2.12836*0.46947 = 0.999 kilometers.
Thus A is closer than B by a - b = 1.424 - 0.999 = 0.425 kilometers = 425 meters, approximately.
Solved.
|
|
|