SOLUTION: Slowtown has a population of 3500 and is losing people at the rate of 150 per year. Boomtown has a population of 1500 and is growing 5% per year. In about how many years will the t

Slowtown population formula  " after t years " is 

    s(t) = 3500 - 150t.


Boomtown population formula  " after t years " is 


    b(t) = .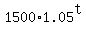


They want you determine the integer number of years t from the condition s(t) = b(t).


If you use equation

    3500 - 150t = ,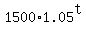

then you will not be able to solve it algebraically: it can be solved only numerically,
using specialized software.


Another way is to calculate functions s(t) and b(t), using your calculator or software 
like Excel spreadsheet.


It is the way which I used in my solution. It produced this table below


  year        Population       Population 
    t         s(t), Slowtown   b(t), Boomtown
              after t years    after t years
                               (rounded to the closest integer value)
 ----------------------------------------------
    0		3500		1500    <<<---=== starting numbers
    1		3350		1575
    2		3200		1654
    3		3050		1736
    4		2900		1823
    5		2750		1914
    6		2600		2010
    7		2450		2111
    8		2300		2216     (*)
    9		2150		2327     (*)
   10		2000		2443


From the table, you see that the populations will become equal 
somewhen in the 9-th year (after 8 years, in the 9-th year).    ANSWER