Question 1196777: Alex is selling tickets. If she charges $100 she can sell 2000 tickets. For every $3 increase in price she sells 20 fewer tickets.
What should she charge to maximize her revenue?
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Alex is selling tickets. If she charges $100 she can sell 2000 tickets.
For every $3 increase in price she sells 20 fewer tickets.
What should she charge to maximize her revenue?
~~~~~~~~~~~~~~~~
After increasing the price n times, the price per ticket is 100+3n dollars,
but the number of sold tickets is 2000-20n.
Thus, after changing the price n times, the revenue is
R(n) = (2000-20n)*(100+3n) = 200000 - 2000n + 6000n - 60n^2 = -60n^2 + 4000n + 200000. (1)
We want to find "n" in a way to maximize quadratic function (1).
+-------------------------------------------------------------------+
| The maximum is at n = "  ", where "a" |
| is the coefficient at n^2 and "b" is the coefficient at n. |
+-------------------------------------------------------------------+
In our problem, a= -60, b= 4000, so the desired n is
n = ", where "a" |
| is the coefficient at n^2 and "b" is the coefficient at n. |
+-------------------------------------------------------------------+
In our problem, a= -60, b= 4000, so the desired n is
n = 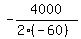 = = 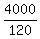 = =  = = 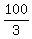 = 33 = 33 .
Next, the number of n in this problem/solution not necessary should be integer,
but the numbers 100+3n and 2000-3n must be integer numbers, due to their meaning.
(100+3n must be integer number of cents, at least.)
We have 100+3n = 200 is still integer, but 200-20n is not integer at n= 33 .
Next, the number of n in this problem/solution not necessary should be integer,
but the numbers 100+3n and 2000-3n must be integer numbers, due to their meaning.
(100+3n must be integer number of cents, at least.)
We have 100+3n = 200 is still integer, but 200-20n is not integer at n= 33 .
THEREFORE, we should test the closest integers n= 33 and n= 34 as possible candidates.
We have the revenue R(33) = -60*33^2 + 4000*33 + 200000 = 266660 dollars,
the revenue R(34) = -60*34^2 + 4000*34 + 200000 = 266640 dollars.
The revenue R(33) is higher, so we choose n= 33 as the number of increases.
It gives the optimum price 100 + 33*3 = 199 dollars.
ANSWER. Optimum price is 199 dollars per ticket. .
THEREFORE, we should test the closest integers n= 33 and n= 34 as possible candidates.
We have the revenue R(33) = -60*33^2 + 4000*33 + 200000 = 266660 dollars,
the revenue R(34) = -60*34^2 + 4000*34 + 200000 = 266640 dollars.
The revenue R(33) is higher, so we choose n= 33 as the number of increases.
It gives the optimum price 100 + 33*3 = 199 dollars.
ANSWER. Optimum price is 199 dollars per ticket.
Solved.
---------------
To learn about finding the minimum/maximum of a quadratic function, see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
I advise you to look into many other lessons in this topic - you will find there
a lot of similar problems solved - - - to make your horizon wider.
|
|
|