Question 1185489: Hi
Arthur and Sam shared some cards. If Arthur gave 20 to Sam they would have the same number of cards.
If Sam gave Arthur 10 cards the ratio of cards Arthur had to Sam is 2 to 1. How many cards did Arthur have at the end.
My sons answer is 110 the textbook is 120.
Thanks
Found 4 solutions by josgarithmetic, ikleyn, MathTherapy, greenestamps:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hi
Arthur and Sam shared some cards. If Arthur gave 20 to Sam they would have the same number of cards.
If Sam gave Arthur 10 cards the ratio of cards Arthur had to Sam is 2 to 1. How many cards did Arthur have at the end.
My sons answer is 110 the textbook is 120.
Thanks
~~~~~~~~~~~~~~~
The question is posed INCORRECTLY in this problem.
They really DID NOT make any change/exchange.
All their changes/exchanges, described in the problem, were VIRTUAL, NOT real.
So, it MAKES no SENSE to ask " how many cards did Artur have at the end ".
The only question which MAKES SENSE is " how many cards does Artur have ?"
I can not believe, that a peer edited/reviewed textbook may have such FAULTY posed problem.
------------
Do not forget to post your " THANKS " to me for my attentive reading and pointing you NONSENSE in this so called " problem ".
It is clear and it is OBVIOUS to me that the " problem " is recovered from a GARBAGE BIN source.
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi
Arthur and Sam shared some cards. If Arthur gave 20 to Sam they would have the same number of cards. If Sam gave Arthur 10 cards the ratio of cards Arthur had to Sam is 2 to 1. How many cards did Arthur have at the end.
My sons answer is 110 the textbook is 120.
Thanks
The statement of the problem is AMBIGUOUS!
If it's CONTINUOUS, then Arthur will have 40 cards at the end.
However, the number at the end is 120, if it's NOT CONTINUOUS and the problem is written as follows: Arthur and Sam shared some cards. If Arthur
gave 20 to Sam they would have the same number of cards. HOWEVER, if Sam gave Arthur 10 cards the ratio of cards Arthur had to Sam is 2 to 1.
How many cards did Arthur have at FIRST. the end.
The "110" cards for Arthur at the end, that your son got, was actually what Arthur started with, not what he would've ended up with. At the same time,
Sam started with 70 cards.
When you SUBTRACT the 20 that Arthur gave Sam, from the 110 he started with, Arthur would've then ended up with 110 - 20 = 90. At the same time, Sam's 70
cards would've become 70 + 20 = 90. As seen they both would've had the same number of cards (90) after this exchange.
However, when you ADD the 10 that Arthur would've received from Sam, to the 110 he started with, Arthur would've ended up with 110 + 10 =
120 (The answer to the problem). At the same time, after giving Arthur 10 cards, Sam's 70 cards would've become 70 - 10 = 60.
As seen directly above, Arthur's count of 120 to Sam's count of 60 would've yielded a  So, Arthur ends up with 90 if 1st scenario is applied, and with 120 if the 2nd one is! Therefore, the correct question should be how many he STARTED with,
since that number never changes, regardless of the number of exchanges.
So, Arthur ends up with 90 if 1st scenario is applied, and with 120 if the 2nd one is! Therefore, the correct question should be how many he STARTED with,
since that number never changes, regardless of the number of exchanges.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The problem is indeed very poorly stated. It would be wrong if the statement of the problem in the textbook is exactly as you how it.
And the textbook answer you show is wrong....
Arthur and Sam shared some cards.
If Arthur gave 20 to Sam they would have the same number of cards.
If Sam gave Arthur 10 cards the ratio of cards Arthur had to Sam 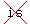 would be 2 to 1. would be 2 to 1.
How many cards did Arthur have? 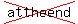
Indeed, as one of the tutors says, asking how many cards Arthur had "at the end" is misleading, because no actual exchanges of cards were made.
For the same reason, the interpretation by the other tutor that the two exhanges actually took place one after the other is not right.
So here is the way I see the problem -- apparently the same way your son saw it, because his answer is right.
Let A = # of cards Arthur has
Let S = # of cards Sam has
(1) A-20 = S+20 if Arthur gave Sam 20 cards, they would have the same number of cards
(2) A+10=2(S-10) if Sam gave Arthur 10 cards, Arthur would have twice as many cards as Sam
There are many different ways to solve the pair of equations to find the answer to the problem. I solved (2) for A and substituted in (1):
A+10=2(S-10)
A+10=2S-20
A=2S-30
2S-30-20=S+20
S=70
A=2S-30=140-30=110
ANSWER: Arthur had 110 cards
CHECK:
Arthur started with 110 cards and Sam started with 70
If Arthur gave Sam 20 cards, they would both have the same number, 90
If Sam gave Arthur 10 cards, Arthur would have 120 and Sam would have 60; 120 is twice 60
All the conditions are satisfied; our answer is correct
-----------------------------------------------------------------------
Another tutor, while I was writing my response, pointed out that Arthur would end up with 120 cards if the second described exchange -- and ONLY the second one -- actually took place.
If that is the interpretation that is intended, so that the answer 120 is the intended answer, then the level of sloppiness in the presentation of the problem is even worse. The statements regarding the two exchanges start with "If Arthur gave Sam... and "If Sam gave Arthur..." -- clearly indicating that NEITHER exchange actually took place.
----------------------------------------------------------------------------
I have seen your message that the problem you posted was taken exactly as given in your textbook.... Neither you nor I can do anything about that.
|
|
|