SOLUTION: Verify that the hypotheses of the Mean Value Theorem are satisfied on the given interval and find all values c that satisfies the conclusion of the theorem if g(x) = x + 1/x, 3 =<

    In calculus, the Extreme Value Theorem states that if a real-valued function f is continuous on 

    the closed interval [a,b], then f must attain a maximum and a minimum, each at least once. 

So, the function is assumed to be CONTINUOUS.


The given function is the sum of two elementary functions,  x  and  .


Each of the two functions is continues on the given interval, as it is known from Calculus.


Therefore, the sum of these functions is continue on the given interval.


It proves the statement.


To answer the last question, you need to solve this quadratic equation 

    x + 1/x = c.


Reduce it to the standard form


    x^2 + 1 = cx

    c^2 - cx + 1 = 0


Calculate the discriminant

    d = .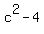


The equation is solvable in real numbers if and only if  d >= 0, which is

    c^2 >= 4,

giving

    c <= -2   OR   c >= 2.     (1)


Since our function g(x) = x +   is always positive on the given interval,  

the inequality (1)  for "c" is reduced to

    c >= 2.



The plot below illustrate the function



    


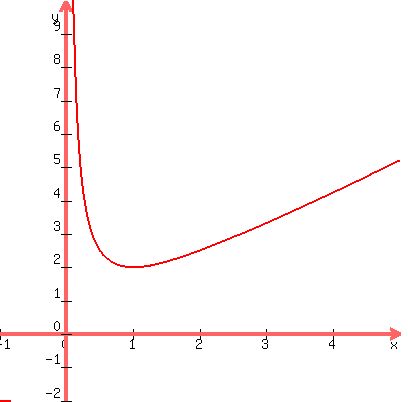            Plot y = x + 1/x


Next, to get the final description for the range of "c"-values, we should evaluate the function at the ends of the interval


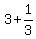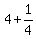    g(3) =  = 1 ;  g(4) =  = 4 .


Now we select the smallest and the greatest values of these two end-points, which are  3  and  4 .


In this way, we obtain inequalities for "c" in the FINAL form


        3  <= c <= 4 .