Question 1169800: Hi
John has 36 coins comprising 20c 50c and $1 coins. He has twice as many $1 coins as 20c coins and the value of the 50c coins $4.40 more than the total value of the 20c coins.
How many $1 coins does he have.
Thanks
Found 5 solutions by Theo, josgarithmetic, ikleyn, greenestamps, MathTherapy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! well, i got an answer, but it's not what you would expect, since the number of coins is not an integer, even though the sum of the number of coins is equal to 36.
but it does work out and i can't get it to work out any other way.
here's what i did.
let a = the number of 20 cents coins.
let b = the number of 50 cent coins.
let c = the number of 1 dollar coins.
the value of the 20 cent coins is 20 * a.
the value of the 50 cent coins is 50 * b.
the value of the 1 dollar coins is 100 * c.
this is because 1 dollar is equal to 100 cents.
you are given that the number of 1 dollar coins is equal to 2 times the number of 20 cent coins.
this leads to the equation:
c = 2 * a
you are given that the value of the 50c coins is equal to $4.40 more than the total value of the 20c coins.
this leads to the equation:
50 * b = 20 * a + 440
4 dollars and 40 cents is converted to 440 cents in that equation to keep the denominations the same for all coins.
you are given that the sum of the number of coins is 36.
this leads to the equation:
a + b + c = 36
since c = 2 * a, solve for a to get a = c/2.
since 50 * b = 20 * c + 440, solve for b to get b = (20 * c + 440)/50
replace a and b in the equation of a + b + c = 36 to get:
c/2 + (20 * c + 440)/50 + c = 36
multiply both sides of this equation by 50 to get:
25 * c + 20 * c + 440 + 50 * c = 1800
combine like terms and subtract 440 from both sides of the equation to get:
95 * c = 1360.
solve for c to get:
c = 14.31578947.
since a = c/2, you get:
a = 7.157894737
since b = (20 * c + 440)/50, you get:
b = 14.52631579
a + b + c = 7.157894737 + 14.52631579 + 14.31578947 = 36.
since the sum of the number of coins is 36, that requirement is satisfied.
c = 2 * a becomes 14.31578947 = 2 * 7.157894737 which becomes 14.31578947 = 14.31578947, so that requirement is satisfied.
50 * b = 20 * c + 440 becomes 50 * 14.52631579 = 20 * 14.31578947 + 440 which becomes 726.3157895 = 726.315789, so that requirement is satisfied.
all the requirements of the problem are satisfied, so the solution is:
number of 20 cent coins is 7.157894737
number of 50 cent coins is 14.52631579
number of 1 dollars coins is 14.31578947
not what you would expect, but that's the answer.
i'm pretty sure i did the problem correctly, based on the way the problem was stated.
my understanding could be wrong, or the problem was simply not presented correctly.
i expected an integer answer for the number of coins, but didn't get it.
that's unfortunate, but i went through all the steps required to solve this problem the way that i normally do and i'm fairly confident that i did nothing wrong.
that, of course, remains to be seen.
let me know if you have any questions regarding my solution to your problem.
theo
Answer by josgarithmetic(39616)  (Show Source):
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
Let x be the number of the 20c coins.
Then the number of the $1 coins is 2x, and the number of the 50c coins is (36-x-2x) = 36-3x.
From the condition, you have this equation
50*(36-3x) = 20x + 440 cents.
Solve it
1800 - 150x = 20x + 440
1800 - 440 = 20x + 150x
1360 = 170x
x = 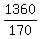 = 8.
Thus the number of the 20c coins is 8.
Hence, the number of the $1 coins is twice as many, i.e. 16. ANSWER
The problem is easily solved using one single unknown and one single equation.
Answer by greenestamps(13198)  (Show Source):
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website!
Hi
John has 36 coins comprising 20c 50c and $1 coins. He has twice as many $1 coins as 20c coins and the value of the 50c coins $4.40 more than the total value of the 20c coins.
How many $1 coins does he have.
Thanks
Theo is CONFUSED, and the fact that he makes these problems so COMPLEX when they don't have to be, has more than likely led him down the "WRONG-ANSWER" path. Hence, just IGNORE his response!
Also IGNORE the other response that brings in UNNECESSARY fractions, which most people dread dealing with!
Let number of 20c coins be T
Then he has 2T, $1 coins, and 36 - (T + 2T), or 36 - 3T, 50c coins
We then get: .5(36 - 3T) = .2T + 4.4
18 - 1.5T = .2T + 4.4
- 1.5T - .2T = 4.4 - 18
- 1.7T = - 13.6
Number of 20c coins, or 
Number of $1 coins:  .
That's ALL!!
|
|
|
