SOLUTION: Hi Bob bought forks and spoons in the ratio of 4:3 respectively. They were bought for 156 dollars. The spoons cost 50 cents more than each fork. The amount he spent on the fork

Let x be the amount spent on the spoons.

Then the amount spent on the forks is (x+12).


The total amount equation is


    x + (x+12) = 156

    2x         = 156 - 12 = 144

    x                     = 72  dollars (spent on the spoons).    ANSWER

Let F be the number of forks.

Then the number of spoons is  .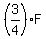


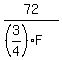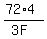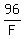Each spoon costs   =  =   dollars.

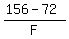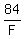Each fork  costs   =   dollars.


The difference of individual prices is 50 cents, or 0.5 dollars


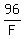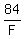     -  = 0.5,   or


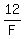            = 0.5.


It implies  F = 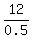 = 24.    It is the number of forks. 


Then the number of spoons is 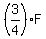  =  = 3*6 = 18.