SOLUTION: A survey of 538 adults aged 18-24 year olds was conducted in which they were asked what they did last Friday night. It found: 175 watched TV 180 hung out with friends 198 ate

You are given an universal set U of 538 elements.

You are given 3 subsets

    T  of 175 elements

    F  of 180 elements

    P  of 198 elements


You are given the set of their triple intersection TFP of 33 elements.


You are given their in-pairs intersections with the triple intersection   from them

    TPo  with 43 elements (it is the intersection T and P with the TFP cut from it;  TPo means (T and P only);

    TFo  with 43 elements (it is the intersection T and F with the TFP cut from it;  TFo means (T and F only);

    FPo  with 49 elements (it is the intersection F and P with the TFP cut from it;  FPo means (F and P only).


My first step is to restore in-pair intersections  TP, TF an FP.

It easy to do by adding 33 elements of the triple intersection TFP to them:


    TP has 43 + 33 = 76 elements;

    TF has 43 + 33 = 76 elements;

    FP has 49 + 33 = 82 elements.


Next I will apply the REMARCABLE formula for the union of three subsets in the universal set

    n(T U F U P) = n(T) + n(F) + n(P) - n(TF) - n(TP) - n(FP) + n(TPP).


Two letters mean in-pair intersections; three letters mean a triple intersection.


Substitute the known values into the formula.

    n(T U F U P) = 175 + 180 + 198 - 76 - 76 - 82 + 33 = 352.


Hence, the rest  538 - 352 = 186 do not make any of the three activities last Friday night.   ANSWER

With P being the number that ate pizza, T being the number that watch TV, and F being the number that hung out with friends, we get the following Venn Diagram: .

With P = 198, 

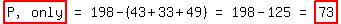With T = 175, 

With F = 180, 

With 538 being surveyed, we get number that didn’t participate in any of the 3 activities as: 
.