Question 1163839: A,B, and C make widgets. A alone needs 10 days. If A and B work together, they
need 6 days. B and C need 8 days. A,B, and C work together. when they finish,
A made 240 widgets more than C did. How many widgets did C make?
Found 3 solutions by Theo, ikleyn, Edwin McCravy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let w = the number of widgets produced.
let a = the rate that A makes widgets.
let b = the rate that B makes widgets.
let c = the rate that c makes widgets.
rate * time = quantity
you are given that A can make w widgets in 10 days.
the formula becomes a * 10 = w
solve for a to get a = w/10
you are given that A and B can make w widgets in 6 days when they work together.
therefore (a + b) * 6 = w
solve for a + b to get a + b = w/6
since a = w/10, the formula becomes w/10 + b = w/6
solve for b to get b = w/6 - w/10 = 10w/60 - 6w/60 = 4w/60 = w/15
you are given that B and C can make w widgets in 8 days when they work together.
therefore (b + c) * 8 = w
solve for b + c to get b + c = w/8
since b = w/15, the formula becomes w/15 + c = w/8
solve for c to get c = w/8 - w/15 = 15w/120 - 8w/120 = 7w/120
your rates for A, B, and C are:
a = w/10
b = w/15
c = 7w/120
when all 3 work together, the formula becomes:
(a + b + c) * T = w
this becomes (w/10 + w/15 + 7w/120) * T = w
this becomes 27w/120 * T = w
solve for T to get T = w * 120/27w = 120/27 days
the contribution of A to w is equal to w/10 * 120/27 = 120/270 * w
the contribution of B to w is equal to w/15 * 120/27 = 120/405 * w
the contribution of C to w is equal to 7w/120 * 120/27 = 7/27 * w
the total contribution is 120/270 * w + 120/405 * w + 7/27 * w = w
the contribution of A is 240 more widgets than the contribution of C.
if you let x = the number of widgets that A contributes and y = the number of widgets that C contributes, you get x = y + 240
subtract y from both sides of this equation to get x - y = 240
since A contributes 120w/270 widgets and C contributes 7w/27 widgets, then x = 120w/270 and y = 7w/27, so you get 240 = 120w/270 - 7w/27
solve for w to get w = 1296
what this says is that, when A and B and C work together, they make 1296 widgets in 120/27 days.
from above:
the contribution of A to w is equal to w/10 * 120/27 = 120/270 * w
the contribution of B to w is equal to w/15 * 120/27 = 120/405 * w
the contribution of C to w is equal to 7w/120 * 120/27 = 7/27 * w
since w = 1296, these formulas become:
the contribution of A to 1296 is equal to 1296/10 * 120/27 = 576
the contribution of B to 1296 is equal to 1296/15 * 120/27 = 384
the contribution of C to 1296 is equal to 7*1296/120 * 120/27 = 336
the contribution of A is 240 more than the contribution of C.
since the contribution of C is 336, then 336 + 240 = 576.
your solution is that C made 336 widgets, assuming i did all of the above correctly.
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A,B, and C make widgets. A alone needs 10 days. If A and B work together, they need 6 days. B and C need 8 days.
A,B, and C work together. when they finish, A made 240 widgets more than C did. How many widgets did C make?
~~~~~~~~~~~~~~~
From the condition, rate of work for A is  of the job per day;
the combined rate of work of A and B working together is of the job per day;
the combined rate of work of A and B working together is  of the job per day.
Hence, the individual rate of B is of the job per day.
Hence, the individual rate of B is  - -  = =  = =  of the job per day.
Next, the combined rate of work of B and C working together is of the job per day.
Next, the combined rate of work of B and C working together is  of the job per day.
Hence, the individual rate of C is of the job per day.
Hence, the individual rate of C is  - -  = = 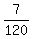 of the job per day.
Then the combined rate of A, B and C, working together, is of the job per day.
Then the combined rate of A, B and C, working together, is
 + +  + + 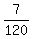 = =  = =  = =  .
It means that they complete the job in .
It means that they complete the job in  days, working all the three together.
During this time, A made days, working all the three together.
During this time, A made  = =  = =  of the job, while C made of the job, while C made 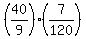 = =  of the job.
If w is the total number of widgets then the contribution of A is of the job.
If w is the total number of widgets then the contribution of A is 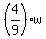 widgets, while the contribution of C is widgets, while the contribution of C is  widgets.
We are given that this difference, widgets.
We are given that this difference, 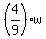 - -  is 240 is 240
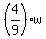 - -  = 240, or = 240, or
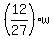 - -  = 240 = 240
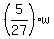 = 240
w = = 240
w = 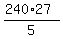 = 1296.
Hence, C made = 1296.
Hence, C made 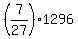 = 336 widgets. ANSWER = 336 widgets. ANSWER
Solved.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I added that they needed to make N widgets to make the question clearer.
A,B, and C make widgets, AND THEY NEED TO MAKE N WIDGETS. A alone needs 10
days TO MAKE N WIDGETS. If A and B work together, they need 6 days TO MAKE N
WIDGETS. B and C need 8 days TO MAKE N WIDGETS. A,B, and C work together TO
MAKE N WIDGETS. When they finish MAKING N WIDGETS, A made 240 widgets more
than C did. How many widgets did C make?
Let the total number of widgets that need be made = N.
Let A's rate be x widgets/day.
A alone needs 10 days TO MAKE N WIDGETS.
So 10x = N
If A and B work together, they need 6 days TO MAKE N WIDGETS
Let B's rate be y widgets/day.
So 6x + 6y = N
6x + 6y = 10x
-4x + 6y = 0
6y = 4x
y = 4x/6
y = 2x/3
B and C need 8 days TO MAKE N WIDGETS.
So 8y + 8z = N
8y + 8z = 10x
4y + 4z = 5x
4(2x/3) + 4z = 5x
8x/3 + 4z = 5x
8x + 12z = 15x
-7x + 12z = 0
12z = 7x
z = 7x/12
A,B, and C work together TO MAKE N WIDGETS.
Let their time to make N widgets be K days.
So Kx + Ky + Kz = N
Kx + K(2x/3) + K(7x/12) = 10x
12Kx + 8Kx + 7Kx = 120x
27Kx = 120x
27K = 120
K = 40/9
When they finish MAKING N WIDGETS, A made 240 widgets more than C did.
Kx = Kz + 240
(40/9)x = (40/9)(7x/12) + 240
Divide through by 40
(1/9)x = (1/9)(7x/12) + 6
Multiply through by 108
12x = 7x + 648
5x = 648
x = 648/5
y = 2(648/5)/3
y = 432/5
z = 7x/12
z = 7(648/5)/12
z = 378/5
How many widgets did C make?
C worked for 40/9 days at the rate of 378/5 widgets/day, so he made
(40/9)(378/5) = 336 widgets.
That's the answer. But to answer all questions that could have been asked
in order to check:
A worked for 40/9 days at the rate of 648/5 widgets/day, so he made
(40/9)(648/5) = 576 widgets. (which is 240 more than the 336 A made)
B worked for 40/9 days at the rate of 432/5 widgets/day, so he made
(40/9)(432/5) = 384 widgets.
So N, the number of widgets they needed to make was 336+576+384 = 1296
widgets.
Edwin
|
|
|