.
We are given that the half-life period is 78 years; therefore, we can write
p(t) = 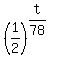 , (1)
where p(t) is the remaining mass fraction. (It is the standard radioactive decay model in terms of half-life period).
The problem asks to determine the time "t" when p(t) = 0.6.
In this case, the equation (1) takes the form
0.6 =
, (1)
where p(t) is the remaining mass fraction. (It is the standard radioactive decay model in terms of half-life period).
The problem asks to determine the time "t" when p(t) = 0.6.
In this case, the equation (1) takes the form
0.6 = 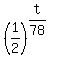 .
Take logarithm base 2 of both sides
.
Take logarithm base 2 of both sides
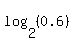 =
= 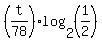 t =
t = 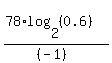 =
= 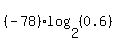 = 57.48 years. ANSWER
= 57.48 years. ANSWER
Solved.
---------------
See the lesson
- Radioactive decay problems
in this site and find there many other similar solved problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
/\/\/\/\/\/\/\/
The lesson to learn from my post is THIS:
If you are given input data in terms of half-life, you do not need to convert your data
into ekt-model. Such conversion is an excessive work and unnecessary calculations.
You can complete all calculations in terms of the half-life model, working consistently with degrees of 2,
which is your base in this case..