SOLUTION: The difference between the squares of two numbers is 8. Three times the square of the first number increased by the square of the second number is 28. Find the numbers.

Let x be the square of the first number, and let y be the square of the seconf number.

Then from the condition, you have these two equations


     x - y =  8     (1)

    3x + y = 28     (2)


Add the equations. You get


    4x = 8 + 28 = 36.   Hence, x = 36/4 = 9.  The first number is   = +/- 3.


Next, substitute x= 9 into the first equation. You will get

    9 - y = 8,  y = 9 - 8 = 1;  hence,  the second number is 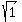  = +/- 1.


ANSWER.  There are 4 pairs of the numbers (first,second) = (3,1),  (3,-1), (-3,1)  and  (-3,-1).