.
The left side is 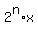 .
The right side is
.
The right side is 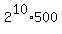 =
= 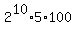 =
= 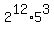 .
Then, comparing the left and the right sides, you get several solutions in integer numbers:
n = 12, x =
.
Then, comparing the left and the right sides, you get several solutions in integer numbers:
n = 12, x = 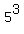 = 125,
n = 11, x = 250,
n = 10, x = 500,
n = 9, x = 1000,
n = 8, x = 2000,
n = 7, x = 4000,
. . . . and so on . . .
n = 0, x =
= 125,
n = 11, x = 250,
n = 10, x = 500,
n = 9, x = 1000,
n = 8, x = 2000,
n = 7, x = 4000,
. . . . and so on . . .
n = 0, x = 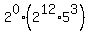 .
.
Solved, answered, explained and completed.