Question 1134623: A license plate has 4 letters, followed by 2 numbers. If repetition is not allowed, how many different license plates can be made?
If repetition is allowed, how many different license plates can be made?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! the license plate has 4 letters followed by 2 numbers.
there are 26 possible letters for each letter position.
there are 10 possible numbers for each number position.
the total number of license plates will be equal to 26^4 * 10^2 = 45,697,600.
if you assume small letters and big letters can be used, then the number of possible license places will be 52^4 * 10^2 = 731,161,600.
nomall, only capital letters are used, so your answer should be 45,697,600 license plates can be issued.
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
If repetition is not allowed, then the number of different licence plates is 26*25*24*23*10*9.
If repetition is allowed, then the number of different licence plates is  .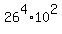
|
|
|
