SOLUTION: Two unit squares share the same center. The overlapping region of the two squares is an octagon with perimeter 3.5. What is the area of the octagon?

Let A, B, C, D, E, F, G, and H be eight consecutive vertices of the octagon.


Draw the segments OA, OB, OC, OD, OE, OF, OG and OH, connecting the vertices with the common center O of the squares.


The segments divide the octagon in 8 triangles.


In these triangles, AB, BC, CD, DE, EF, FG, GH and HA are the bases; the height is    of a unit in all the triangles.


Therefore the area of the octagon is


    Area =  =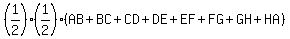

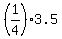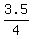         =  =  =  = 0.875 of a square unit.     ANSWER

    (a)  Due to symmetry, all the sides of the octagon  AB, BC, CD, DE, EF, FG, GH and HA  have the same length.


    (b)  This octagon is circumscribed about the circle of the radius 0.5 of a unit with the center at the shared center of the squares.


    (c)  It is not necessary a regular octagon; but its sides all have equal lengths.


    (d)  As for any polygon circumscribed about a circle, its area is half the product of the perimeter and the radius of the circle.