Question 1132885: Question 2
Part A
Maria and Josie are also figuring out the dimensions of the runners’ corral at the start line. To accommodate the number of projected runners, they’ve determined that they need a minimum area of 29,040 square feet in the corral. They have 1,364 feet of temporary fence barriers to set up the corral. They are leaving one end of the rectangular corral open as shown in the image.
https://cdn.app.edmentum.com/EdAssets/5b3899110c584f1a9a3b3a9fa0db6e85?ts=636380088681800000 (copy and paste into url)
When the race is about to start, Maria and Josie will remove the fencing barriers on the start line. Create an inequality that represents the relationship between the area of the space and the length of fencing needed.
Part B
Would a length of 650 feet meet the requirements for the runners’ corral? If so, what would the width be? Justify your response with calculations.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this can be solved graphically as shown below.
you graph the equations of 1364 = 2x + y and 29040 = x * y.
x is the length of the enclosure.
y is the width of the enclosure.
2x + y is the perimeter of the enclosure.
2 lengths and one of the widths is enclosed.
x * y is the area of the enclosure.
you then shade the area of the graph that satisfies the inequalities of:
2x + y <= 1364.
x * y >= 29040.
your graph will look like this.
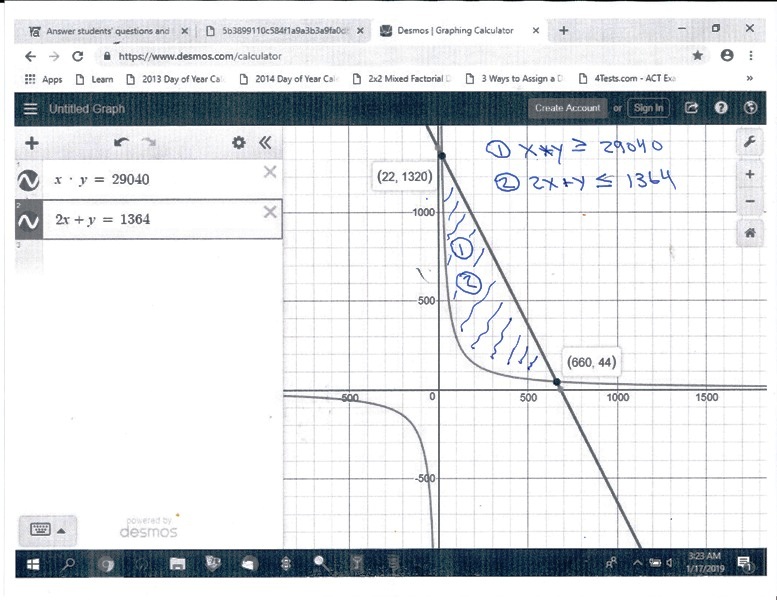
the value of x can go from 22 to 660
the value of y can go from 1320 to 44
these are ordered pairs, so when x = 22, y is 1320, and when x = 660, y = 44.
the value of x can be any value between 22 and 660.
the corresponding value of y will be any value between the intersection of that vertical line on the graph and the curve of the area and the line of the perimeter.
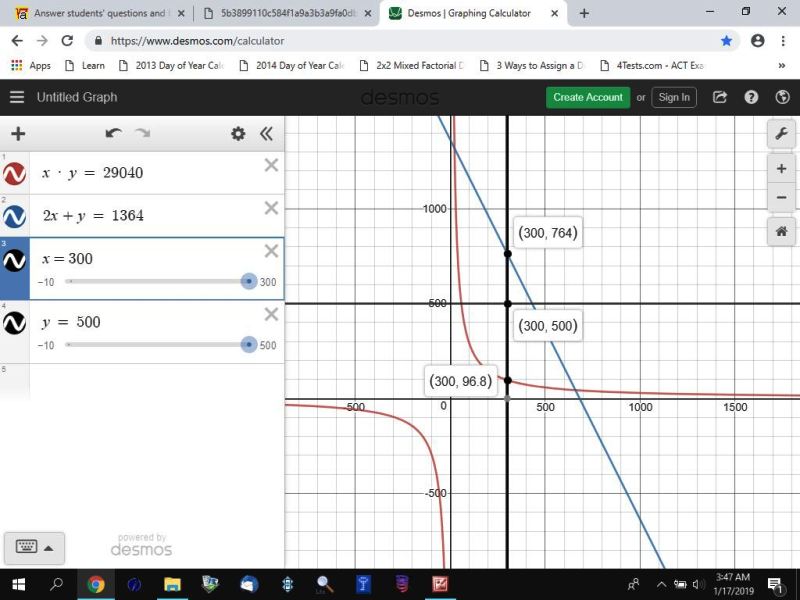
for example, if you pick = 300 and draw it on the graph of the equations of area curve and the perimeter line, you will see that the intersection point with the curve is (300,764) and the intersection point with the line is (300,96.8).
y can be any value between those two values.
for example, when y = 500, the intersection point on the graph is the point (300,500).
that point meets the requirements of the constaints because:
x * y = 300 * 500 = 150000 which is greater than 29040.
2x + y = 600 + 500 = 1100 which is less than 1364.
that graph looks like this.
so you have two inequalities that describe the constraints.
they are:
2x + y <= 1364
x * y >= 29040
x is the length of the enclosure
y is the width of the enclosure.
both constraints have to be satisfied simultaneously.
could 650 feet of fence satisfy the requirements of the problem?
2x + y = 650 does satisfy the constraint that 2x + y <= 1364.
however, what is the area when 2x + y = 650?
solve for y in this equation to get y = 650 - 2x.
the area equation is x * y >= 29040.
replace y with 650 - 2x to get x * (650 - 2x) >= 29040.
put this equation in standard quadratic form to get -2x^2 + 650x - 29040 = 0.
when in this form, you get:
a = -2
b = 650
c = 29040
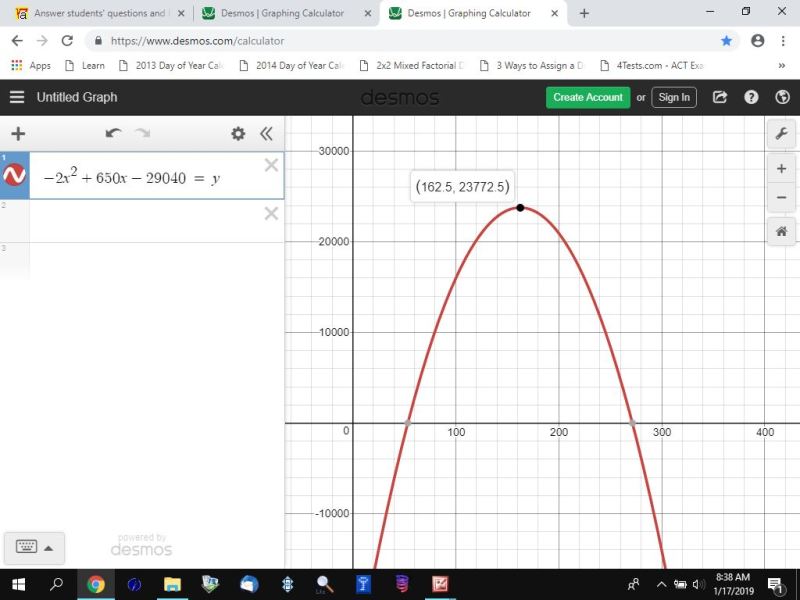
the maximum value of the equation is when x = -b/2a = -650 / -4 = 162.5
when x = = 162.5, y = -2(162.5)^2 + 650 * 162.5 - 29040 = 23772.5 which is less than the required area of greater than or equal to 29040.
the length of fence cannot be 650 feet and satisfy both constraints.
if satisfies the perimeter constraint but doesn't satisfy the area constraint.
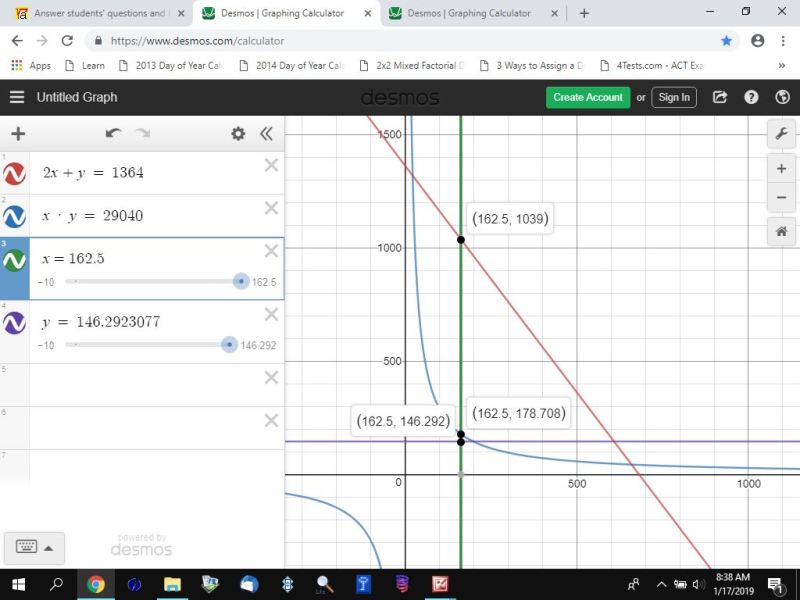
the following 2 graphs illustrate this.
the first graph shows that the maximum value for the area will be 23772.5 when the width is 162.5
you can calculate the length to be 23772.5 / 162.5 = 146.292307.
the second graph shows that the value of y has to be between 1039 and 178.708 for the length and the width to be within the area of feasibility.
since the value of y is 146.292, it falls outside the area of feasibility.
|
|
|